Coordination Compounds 2 Question 49
####51. The correct option(s) regarding the complex $\left[Co(en)\left(NH _3\right) _3\left(H _2 O\right)\right]^{3+}\left(en=H _2 NCH _2 CH _2 NH _2\right)$ is (are)
(2018 Adv.)
(a) It has two geometrical isomers
(b) It will have three geometrical isomers, if bidentate ’en’ is replaced by two cyanide ligands
(c) It is paramagnetic
(d) It absorbs light at longer wavelength as compared to $\left[Co(en)\left(NH _3\right) _4\right]^{3+}$
Show Answer
Answer:
Correct Answer: 51. (a, b, d)
Solution:
- Statement wise explanation is
Statement (a) $\left[Co(en)\left(NH _3\right) _3 H _2 O\right]^{3+}$ have following 2 geometrical isomers.
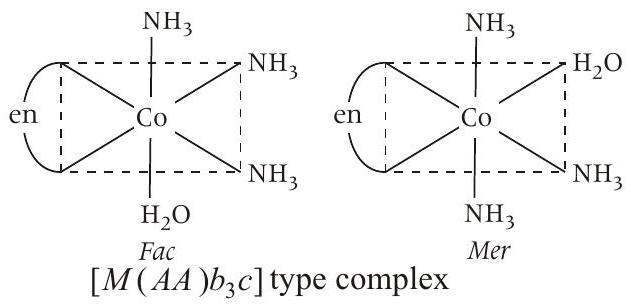
Hence, this is correct statement.
Statement (b) If bidentate ligand ’en’ is replaced by two cyanide ligands then $\left[Co\left(NH _3\right) _3\left(H _2 O\right)(CN) _2\right]^{+}$is formed.
It is $\left[M a _3 b _2 c\right]$ type complex which has following 3 geometrical isomers.
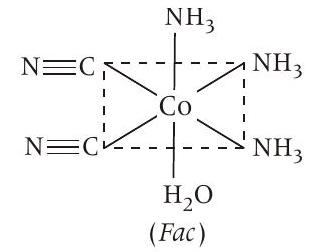
Fac with respect to $NH _3$ and $NH _3$ Mer with respect to $-CN$
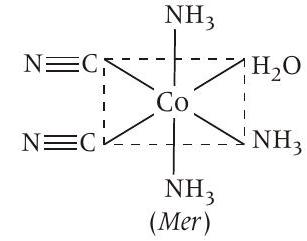
Hence, this statement is also correct.
Statement (c) Co metal has $[Ar] 3 d^{7} 4 s^{2}$ configuration while in $\left[Co(en)\left(NH _3\right) _3\left(H _2 O\right)\right]^{3+}$ it is in +3 oxidation state. Thus, $Co^{3+}$ has $[Ar] 3 d^{6}$ configuration.
$$ Co^{3+}= $$
As $e n$ is a strong ligand, so pairing will occur
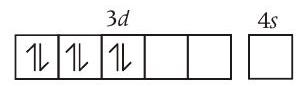
Due to the presence of all paired electrons it show diamagnetic behaviour rather than paramagnetic.
Hence, this statement is incorrect. Statement (d) According to CFT, absorption of light by coordination complexes depends upon CFSE i.e., crystal field splitting energy $\left(\Delta _0\right)$ as
$$ \Delta _0 \propto \frac{1}{\lambda} $$
Among the complexes given $\left[Co(en)\left(NH _3\right) _4\right]^{3+}$ has more $\Delta _0$ value as compared to complex $\left[Co(en)\left(NH _3\right) _3\left(H _2 O\right)\right]^{3+}$. Thus, $\left[Co(en)\left(NH _3\right) _3\left(H _2 O\right)\right]^{3+}$ absorbs the light at longer wavelength for $d-d$ transition.
Hence, this statement is also correct.
Note : For any complex, the value of $\Delta _0$ can be calculated via the difference or gap between $e _g$ and $t _{2 g}$ values.






