SATHEE: Coordination Compounds 2 Question 49

Coordination Compounds 2 Question 49

####51. The correct option(s) regarding the complex ${[C o (e n) {(N H_{3})}_{3} (H_{2} O)]}^{3 +} (e n = H_{2} N C H_{2} C H_{2} N H_{2})$ is (are)

(2018 Adv.)

(a) It has two geometrical isomers

(b) It will have three geometrical isomers, if bidentate ’en’ is replaced by two cyanide ligands

(d) It absorbs light at longer wavelength as compared to ${[C o (e n) {(N H_{3})}_{4}]}^{3 +}$

Show Answer

Answer:

Correct Answer: 51. (a, b, d)

Solution:

Statement wise explanation is

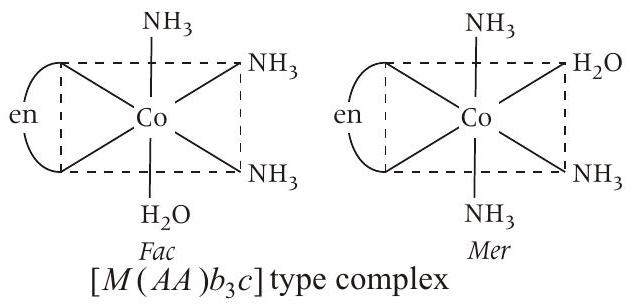
Statement (a) ${[C o (e n) {(N H_{3})}_{3} H_{2} O]}^{3 +}$ have following 2 geometrical isomers.

Hence, this is correct statement.

Statement (b) If bidentate ligand ’en’ is replaced by two cyanide ligands then ${[C o {(N H_{3})}_{3} (H_{2} O) (C N)_{2}]}^{+}$ is formed.

It is $[M a_{3} b_{2} c]$ type complex which has following 3 geometrical isomers.

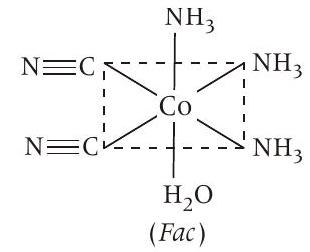
Fac with respect to $N H_{3}$ and $N H_{3}$ Mer with respect to $- C N$

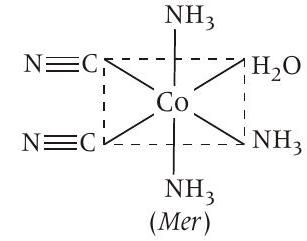
Hence, this statement is also correct.

Statement (c) Co metal has $[A r] 3 d^{7} 4 s^{2}$ configuration while in ${[C o (e n) {(N H_{3})}_{3} (H_{2} O)]}^{3 +}$ it is in +3 oxidation state. Thus, $C o^{3 +}$ has $[A r] 3 d^{6}$ configuration.

$C o^{3 +} =$

As $e n$ is a strong ligand, so pairing will occur

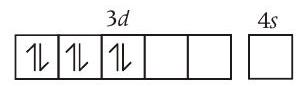
Due to the presence of all paired electrons it show diamagnetic behaviour rather than paramagnetic.

Hence, this statement is incorrect. Statement (d) According to CFT, absorption of light by coordination complexes depends upon CFSE i.e., crystal field splitting energy $(Δ_{0})$ as

$Δ_{0} \propto \frac{1}{λ}$

Among the complexes given ${[C o (e n) {(N H_{3})}_{4}]}^{3 +}$ has more $Δ_{0}$ value as compared to complex ${[C o (e n) {(N H_{3})}_{3} (H_{2} O)]}^{3 +}$ . Thus, ${[C o (e n) {(N H_{3})}_{3} (H_{2} O)]}^{3 +}$ absorbs the light at longer wavelength for $d - d$ transition.