Standard Equation of Parabola

$\quad$ The equation of a standard parabola is $\mathrm{y}^{2}=4 a \mathrm{ax}$, where $\mathrm{a}$ is an arbitrary constant.

Important terms and other forms of a standard parabola

PYQ-2023-Sequence_and_Series-Q14

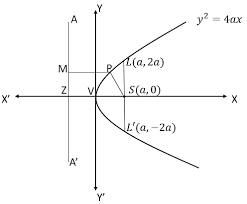
• $SP=PM $ and $ VS=VZ $

• Vertex is at $V(0,0)$

• Focus is at $\mathrm{S}(\mathrm{a}, 0)$

• Directrix is $x+a=0$

• Axis is $y=0$

• Length of latus rectum $=\mathrm{LL}^{\prime}=4 a$

• Ends of the latus rectum are $L(a, 2 a) $ and $ L^{\prime}(a,-2 a)$

• The parametric equation is: $x=a t^{2}, y=2 a t$.

• The other forms of the parabola with latus rectum $4 a$ are $y^{2}=-4 a x, x^{2}=4 a y, x^{2}=-4 a y$

The general equation of a parabola

PYQ-2023-Parabola-Q4

$\quad$ Let $(a, b)$ be the focus $S$, and $lx+m y+n=0$ is the equation of the directrix. Let $P(x, y)$ be any point on the parabola. Then by definition

$$ \mathrm{SP}=\mathrm{PM}$$

$$\Rightarrow \sqrt{(x-a)^{2}+(y-b)^{2}}=\frac{l x+m y+n}{\sqrt{l^{2}+m^{2}}}$$

$$\Rightarrow(x-a)^{2}+(y-b)^{2}=\frac{(l x+m y+n)^{2}}{l^{2}+m^{2}}$$

$$\Rightarrow \mathrm{m}^{2} \mathrm{x}^{2}+\mathrm{l}^{2} \mathrm{y}^{2}-2 \mathrm{lmxy}+(\text{Coefficient of x}) \mathrm{x}+( \text{Coefficient of y}) \mathrm{y}+ \text{Constant }=0$$

$$\Rightarrow(m x-l y)^{2}+2 g x+2 f y+c=0$$

$\quad$ It should be seen that the second degree terms in the general equation of a parabola forms a perfect square.

• The equation of the parabola with axis parallel to the $x$-axis is of the form $x=A y^{2}+B y+C$.
• The equation of the parabola with axis parallel to the $y$-axis is of the form $y=A x^{2}+B x+C$.

Parametric Equations of the Parabola $y^{2}=4 a x$:

$\quad$ The parametric equations of the parabola $y^{2}=4 a x$ are $x=a t^{2}, y=2 a t$, where $I$ is the parameter.

$\quad$ Since the point (at ${ }^{2}$, 2at) satisfies the equation $y^{2}=4 a x$. The parametric coordinates of any point on the parabola are $\left(a t^{2}, 2 a t\right)$.

The position of a Point w.r.t parabola $y^{2}=4 a x$:

$\quad$ Let $P$ be any point $(h, k)$. Now $P$ will lie outside, on or inside the parabola according as $\left(k^{2}-4 a h\right)$ greater than, less than or equal to zero.

Relation between a parabola and a line:

$\quad$ Let the parabola be $y^2 = 4ax$ and the given line be $y = mx + c$. Solving the line and parabola, we get

$$(mx + c)^2 = 4ax$$

$\quad$ i.e.,

$$m^2 x^2 + 2(mc - 2a)x + c^2 = 0$$

$\quad$ This equation being a quadratic in $x$, the discriminant is

$$\Delta = 4(mc - 2a)^2 - 4m^2 c^2 = 16a(a - mc)$$

$\quad$ Hence, the line intersects the parabola in two distinct points if $a > mc$, in one point if $a = mc$, and does not intersect if $a < mc$.

$\quad$ The line $y = mx + \frac{a}{m}$ touches the parabola $y^2 = 4ax$ at the point $\left(\frac{a}{m^2}, \frac{2a}{m}\right)$ for $m \neq 0$.

The Equation Of The Tangent:

PYQ-2023-Parabola-Q1, PYQ-2023-Parabola-Q2, PYQ-2023-Parabola-Q3, PYQ-2023-Parabola-Q5, PYQ-2023-Parabola-Q6, PYQ-2023-Parabola-Q7

• The equation of the tangent at any point $(x_1, y_1)$ on the parabola $y^2 = 4ax$ is $yy_1 = 2a(x + x_1)$.

• The slope of the tangent is $\frac{2a}{y_1}$.

• The equation of the tangent at any point $t$ is $ty = x + at^2$.

• The slope of the tangent is $\frac{1}{t}$.

• Coordinates of the point of intersection of tangents at $t_1$ and $t_2$ is $(at_1t_2, a(t_1 + t_2))$.

• If the chord joining $t_1$ and $t_2$ is a focal chord, then $t_1t_2 = -1$. Hence, if one extremity of a focal chord is $\left(at_1^2, -2at_1\right)$,

  then the other extremity is $\left(\frac{a}{t_1^2}, -\frac{2a}{t_1}\right)$.

The Equation Of The Normal:

PYQ-2023-Parabola-Q4

• The equation of the normal at any point $(x_1, y_1)$ on the parabola $y^2 = 4ax$ is $(y - y_1) = -\frac{y_1}{2a}(x - x_1)$.

• The slope of the normal is $-\frac{y_1}{2a}$.

• The equation of the normal at any point $t$ is $y = -tx + 2at + at^3$.

• The slope of the normal is $-t$.

• Coordinates of the point of intersection of normals at $t_1$ and $t_2$ is $\left[2a + a(t_1^2 + t_2^2 + t_1t_2), -at_1t_2(t_1 + t_2)\right]$.

• If the normal at the point $t_1$ meets the parabola again at $t_2$, then $t_2 = -t_1 - \frac{2}{t_1}$.

Some Standard Results On The Parabola:

• The tangents at the extremities of a focal chord of a parabola intersect at right angles on the directrix.

• The tangent at any point of a parabola bisects the angle between the focal distance of the point and the perpendicular on the directrix from the point.

• The portion of a tangent, to a parabola, cut off between the directrix and the curve, subtends a right angle at the focus.

• The foot of the perpendicular from the focus on any tangent to a parabola lies on the tangent at the vertex.

• If $S$ be the focus of the parabola and tangent and normal at any point $P$ meet its axis $I, T$ and $G$ respectively, then $\mathrm{ST}=\mathrm{SG}=\mathrm{SP}$.

  if the tangent at $\mathrm{P}$ meets the axis in $\mathrm{M}$, then $\angle \mathrm{MSP}=90^{\circ}$.

• If $\mathrm{S}$ be the focus and $\mathrm{SH}$ be perpendicular to the tangent at $\mathrm{P}$, then $\mathrm{H}$ lies on the tangent at the vertex and $\mathrm{SH}^{2}=\mathrm{OS}$. $\mathrm{SP}$

The Equation Of Chord With The Midpoint $(x_{1}, y_{1})$:

$\quad$ The equation of the chord of the parabola $y^2 = 4ax$, whose midpoint is $(x_1, y_1)$, is given by

$$T = S_1$$

$\quad$ where $T \equiv yy_1 - 2a(x + x_1) = 0$ and $S_1 = y_1^2 - 4ax_1 = 0$.

Chord of contact

• If $PA$ and $PB$ be the tangents through point $P(x_1, y_1)$ to the parabola $y^2 = 4ax$, then the equation of the chord of contact $AB$ is

$$yy_1 = 2a(x + x_1) \text{ or } T = 0 \text{ at } (x_1, y_1)$$

• If $P(x_1, y_1)$ be any point lying outside the parabola $y^2 = 4ax$, and the pair of tangents $PA, PB$ can be drawn to it from $P$, then the equation

  of the pair of tangents $PA$ and $PB$ is

$$SS_1 = T^2; \text{ where } S \equiv y^2 - 4ax = 0$$

$$S_1 \equiv y_1^2 - 4ax_1 = 0$$

$$T \equiv yy_1 - 2a(x + x_1) = 0$$

Diameter:

$\quad$ The locus of the middle points of a system of parallel chords is called a diameter.

• If $y = mx + c$ represents a system of parallel chords of the parabola $y^2 = 4ax$, then the equation of the diameter is $y = \frac{2a}{m}$.