Equation of tangent and normal :

$\quad$ Tangent at $\left(x_{1}, y_{1}\right)$ is given by $\left(y-y_{1}\right)=f^{\prime}\left(x_{1}\right)\left(x-x_{1}\right)$; when, $f^{\prime}\left(x_{1}\right)$ is real.

$\quad$ And normal at $\left(x_{1}, y_{1}\right)$ is $\left(y-y_{1}\right)=-\frac{1}{f^{\prime}\left(x_{1}\right)}\left(x-x_{1}\right)$, when $f^{\prime}\left(x_{1}\right)$ is nonzero real.

Tangent from an external point:

PYQ-2023-Hyperbola-Q1

$\quad$ Given a point $P(a, b)$ which does not lie on the curve $y=f(x)$, then the equation of possible tangents to the curve $y=f(x)$, passing through

$\quad$ $(a, b)$ can be found by solving for the point of contact $Q$.

$$f^{\prime}(h)=\frac{f(h)-b}{h-a}$$

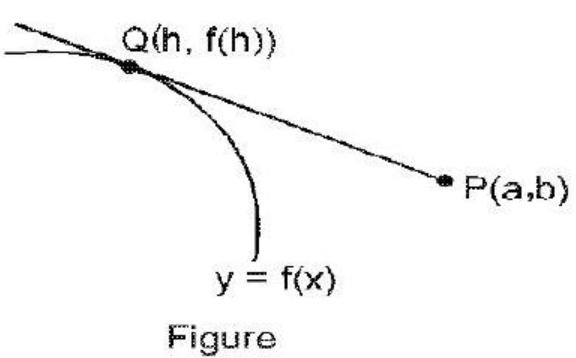
$\quad$ And equation of tangent is $y-b=\frac{f(h)-b}{h-a}(x-a)$

Length of tangent, normal, subtangent, subnormal:

• $\mathrm{PT}=|\mathrm{k}| \sqrt{1+\frac{1}{\mathrm{~m}^{2}}}=$ Length of Tangent

• $\mathrm{PN}=|\mathrm{k}| \sqrt{1+\mathrm{m}^{2}}=\text { Length of Normal }$

• $T M=\left|\frac{k}{m}\right|=$ Length of subtangent

• $\mathrm{MN}=|\mathrm{km}|=$ Length of subnormal.

Angle between the curves:

$\quad$ Angle between two intersecting curves is defined as the acute angle between their tangents (or normals) at the point of intersection of two curves.

$$ \tan \theta=\left|\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\right| $$

Shortest distance between two curves :

$\quad$ Shortest distance between two non-intersecting differentiable curves is always along their common normal. (Wherever defined)

Rolle’s theorem :

$\quad$ If a function $f$ defined on $[a, b]$ is:

$\quad$ (i) continuous on $[a, b]$

$\quad$ (ii) derivable on $(a, b)$ and

$\quad$ (iii) $f(a)=f(b)$,

$\quad$ then there exists at least one real number $c$ between $a$ and $b(a<c<b)$ such that $f^{\prime}(c)=0$

Lagrange’s Mean Value Theorem (LMVT) :

$\quad$ If a function $f$ defined on $[a, b]$ is

$\quad$ (i) continuous on $[a, b]$ and

$\quad$ (ii) derivable on $(a, b)$

$\quad$ then there exists at least one real numbers between a and $b(a<c<b)$ such that $\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)$

Useful formulae of mensuration to remember :

• Volume of a cuboid $=\ell \mathrm{bh}$.

• Surface area of cuboid $=2(\ell b+b h+h \ell)$.

• Volume of cube $=\mathbf{a}^{3}$

• Surface area of cube $=6 a^{2}$

• Volume of a cone $=\frac{1}{3} \pi r^{2} h$.

• Curved surface area of cone $=\pi \mathrm{r} \ell(\ell=$ slant height $)$

• Curved surface area of a cylinder $=2 \pi \mathrm{rh}$.

• Total surface area of a cylinder $=2 \pi r h+2 \pi r^{2}$.

• Volume of a sphere $=\frac{4}{3} \pi r^{3}$.

• Surface area of a sphere $=4 \pi r^{2}$.

• Area of a circular sector $=\frac{1}{2} r^{2} \theta$, when $\theta$ is in radians.

• Volume of a prism $=$ (area of the base) $\times$ (height).

• Lateral surface area of a prism $=$ (perimeter of the base) $\times$ (height).

• Total surface area of a prism $=$ (lateral surface area $)+2$ (area of the base)

$\quad \quad \quad $ (Note that lateral surfaces of a prism are all rectangle).

• Volume of a pyramid $=\frac{1}{3}$ (area of the base) $\times$ height .

• Curved surface area of a pyramid $=\frac{1}{2}$ (perimeter of the base $) \times($ slant height). (Note that slant surfaces of a pyramid are triangles).

The interpretation of derivatives :

$\quad \frac{dy}{dx}$ represents the slope of the tangent.

Slope of the normal = - $\frac{dx}{dy}$

Increasing and decreasing of a function:

PYQ-2023-AOD-Q1, PYQ-2023-AOD-Q10, PYQ-2023-Definite_Integration-Q5

$\quad$ • If f’(x)>0 in x belongs to (a,b) then the function is increasing in the interval (a,b).

$\quad$ • If f’(x)<0 in x belongs to (a,b) then the function is decreasing in the interval (a,b).

Equation of tangent :

• Equation of tangent to the curve y = f(x) at $A(x_1, y_1)$ is given by $y - y_1 = (\frac{dy}{dx})_{(x_1, y_1)} (x-x_1)$

• If the tangent is parallel to the x-axis then, slope will be equal to zero.

• If the tangent is parallel to the y-axis then, slope will be equal to $\infty$.

Some common parametric coordinates on a curve that are useful for differentiation:

• For $x^{2/3} + y^{2/3} = a^{2/3}$, take parametric coordinates $x = a \cos^3 \theta \text{and} y = a sin^3θ$

• For $\sqrt{x} + \sqrt{y} = \sqrt{a}$ take $x = a \cos^4 \theta \text{and} y = a \sin^4θ$

$$\frac{x^n}{a^n} + \frac{y^n}{b^n} =1, \text{~where,}~ x = a (\sinθ)^{2/n} \text{~ and~} y = b (\cosθ)^{2/n}$$

• For $c^2 (x^2 + y^2) = x^2y^2$, take x = c sec θ and y = c cosec θ

Equation of normal:

PYQ-2023-AOD-Q4, PYQ-2023-AOD-Q6, PYQ-2023-Area_Under_Curves-Q12

$\quad$ The equation of the normal at $(x_1, y_1)$ to the curve $y=f(x)$ is given by the following formula:

$$ (y-y_1)=m(x-x_1) \ \text{where} \ m=-\left(\frac{1}{\frac{dy}{dx}}\right) _{(x_1,y_1)} $$

• Some facts regarding the normal :

• Slope of the normal drawn at point $P\left(x_1, y_1\right)$ to the curve $y=f(x)=-\left(\frac{d x}{d y}\right)_{\left(x_1, y_1\right)}$

• If the normal makes an angle of $\theta$ with the positive direction of the $x$-axis, then $-\frac{d x}{d y}=\tan \theta$ or $\frac{d y}{d x}=-\cot \theta$

• If the normal is parallel to the $x$-axis, then $\frac{d x}{d y}=0$ or $\frac{d y}{d x}=\infty$

• If the normal is parallel to the $y$-axis, then $\left(\frac{d x}{d y}\right)=\infty$ or $\frac{d y}{d x}=0$

• If the normal is equally inclined from both the axes or cuts equal intercept, then $-\left(\frac{d x}{d y}\right)= \pm 1$ or $\left(\frac{d y}{d x}\right)= \pm 1$

• The length of the perpendicular from the origin to the normal is $P^{\prime}=\left|\frac{x_1+y_1\left(\frac{d y}{d x}\right)}{\sqrt{1+\left(\frac{d y}{d x}\right)^2}}\right|$

Length of tangent, normal, subtangent and subnormal :

• Tangent $ \text { PT }=M P \operatorname{cosec} \theta=y \sqrt{1+\cot ^2 \theta}=\left|\frac{y \sqrt{1+\left(\frac{d y}{d x}\right)^2}}{\frac{d y}{d x}}\right| $

• Subtangent $ \mathrm{TM}=\mathrm{MP} \cot \theta=\left|\frac{\mathrm{y}}{(\mathrm{dy} / \mathrm{dx})}\right| $

• Normal $ \text { GP }=\text { MP sec } \theta=y \sqrt{1+\tan ^2 \theta}=\left|y \sqrt{1+\left(\frac{d y}{d x}\right)^2}\right| $

• Subnormal $ M G=M P \tan \theta=\left|y\left(\frac{d y}{d x}\right)\right| $

Approximation using differentiation:

$\quad$ The approximate value of y when the increment ∆ x is given to the independent variable x in y = f(x) is:- $$y + ∆y = f(x + ∆x) = f(x) + \frac{dy}{dx} ∆x\Rightarrow f(x + ∆x) = f(x) + f’(x) ∆x$$

Maxima and Minima of functions of one variable :

PYQ-2023-AOD-Q2, PYQ-2023-AOD-Q3, PYQ-2023-AOD-Q7, PYQ-2023-AOD-Q8, PYQ-2023-AOD-Q9, PYQ-2023-AOD-Q10, PYQ-2023-AOD-Q13

Let $\mathrm{c}$ be a point in a domain $\mathrm{D}$ of a function $\mathrm{f}$. Then $\mathrm{f}(\mathrm{c})$ is the $\Rightarrow$ absolute maximum value of $\mathrm{f}$ on $\mathrm{D}$ if $f(c) \geq f(x)$ for all $\mathrm{x}$ in $\mathrm{D}$. $\Rightarrow$ absolute minimum value of $\mathrm{f}$ on $\mathrm{D}$ if $f(c) \leq f(x)$ for all $\mathrm{x}$ in $\mathrm{D}$.

Definition:

Let $\mathrm{c}$ be a point in a domain $D$ of a function $f$. Then $f(c)$ is the $\Rightarrow$ local maximum value of $\mathrm{f}$ if $f(c) \geq f(x)$ when $\mathrm{x}$ is near $\mathrm{c}$. $\Rightarrow$ local minimum value of $\mathrm{f}$ if $f(c) \leq f(x)$ when $\mathrm{x}$ is near $\mathrm{c}$.

Critical Point:

A critical point of a function $f$ is a point $c$ in the domain of $f$ such that either $f^{\prime}(c)=0$ or $f^{\prime}$ (c) does not exists. If $f$ has local maximum value or minimum value at $c$, then $c$ is a critical point of $f$.

Rolle’s Theorem:

Let $\mathrm{f}$ be a function that satisfies the following three condition

1. $f$ is continuous on the closed interval $[a, b]$
2. $f$ is differentiable on the open interval $(a, b)$
3. $f(a)=f(b)$

Then there exists a number $\mathrm{c}$ in $(a, b)$ such that $f^{\prime}(c)=0$

The first derivative test:

Definition:

Suppose that $\mathrm{c}$ is a critical number of a continuous function $\boldsymbol{f}$.

(a) If $f$ ’ changes from positive to negative at $\mathrm{c}$, then $f$ has a local maximum at $\mathrm{c}$. (b) If $f$ ’ changes from negative to positive at $\mathrm{c}$, then $f$ has a local minimum at $\mathrm{c}$. (c) If $f^{\prime}$ does not change sign at $\mathrm{c}$ ( for example if $f^{\prime}$ is positive on both sides of $\mathrm{c}$ or negative on both sides), then $f$ has no local maximum or minimum at $\mathrm{c}$.

The Second Derivative Test:

Definition:

Suppose $f^{\prime \prime}$ is continuous near $\mathrm{c}$,

(a) If $f^{\prime}(c)=0$ and $f^{\prime \prime}(c)>0$, then fhas a local minimum at $c$. (b) If $f^{\prime}(c)=0$ and $f^{\prime \prime}(c)<0$, then $\mathrm{f}$ has a local maximum at $\mathrm{c}$.