Area Under Curves
Area under curves Formula :
PYQ-2023-Area_Under_Curves-Q1, PYQ-2023-Area_Under_Curves-Q2, PYQ-2023-Area_Under_Curves-Q3, PYQ-2023-Area_Under_Curves-Q4, PYQ-2023-Area_Under_Curves-Q5, PYQ-2023-Area_Under_Curves-Q6, PYQ-2023-Area_Under_Curves-Q7, PYQ-2023-Area_Under_Curves-Q8, PYQ-2023-Area_Under_Curves-Q9, PYQ-2023-Area_Under_Curves-Q10, PYQ-2023-Area_Under_Curves-Q11, PYQ-2023-Area_Under_Curves-Q13, PYQ-2023-Probability-Q12, PYQ-2023-Hyperbola-Q3
- Area bounded by a curve with $\mathbf{x}$ - axis:
$$A=\int_a^b y d x=\int_a^b f(x) d x$$
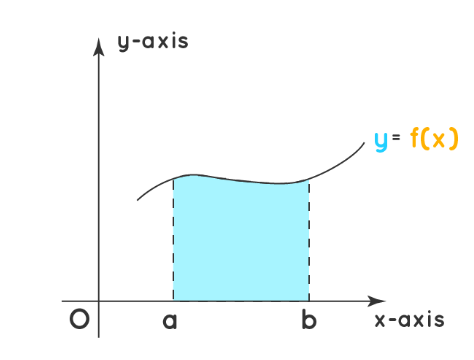
$\quad$
- Area bounded by a curve with $y$-axis:
$$A = \int_a^b x d y=\int_a^b f(y) d y$$
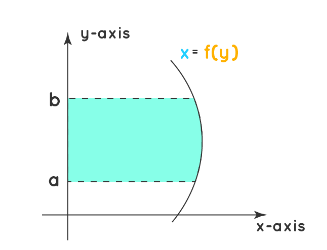
$\quad$
- Area of a curve in parametric form: ($y=g(t), x=f(t)$) $$A=\int_a^b y d x=\int_{t_2}^{t_1} g(t) f^{\prime}(t) d t$$
$\quad$
- Area above and below the x-axis:
$$ A=\left|\int_a^b f(x) d x\right|+\left|\int_b^c f(x) d x\right| $$;
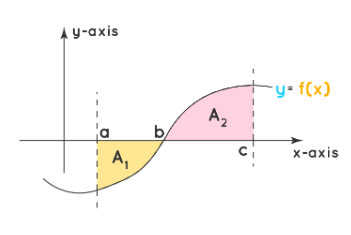
$\quad$
-
Area between two curves:
-
Area enclosed between two curves intersecting at two different points: $$ \text { A}=\int_a^b\left(y_1-y_2\right) d x=\int_a^b\left[f(x)-g(x)\right] d x $$
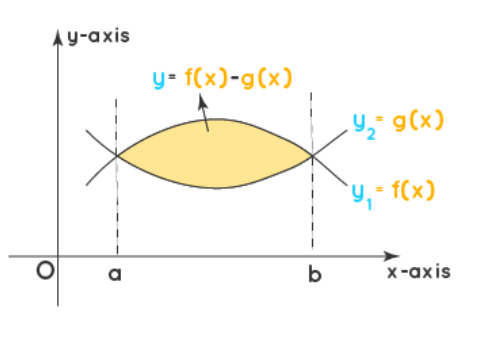
$\quad$
- Area enclosed between two curves intersecting at one point and the $x$-axis: $$ \text { A }=\int_a^\alpha f(x) d x+\int_\alpha^b g(x) d x $$
$\quad$
- Area bounded by two intersecting curves and lines parallel to $\mathrm{y}-$ axis: $$ \text { A }=\int_a^c(f(x)-g(x)) d x+\int_c^b(g(x)-f(x)) d x $$
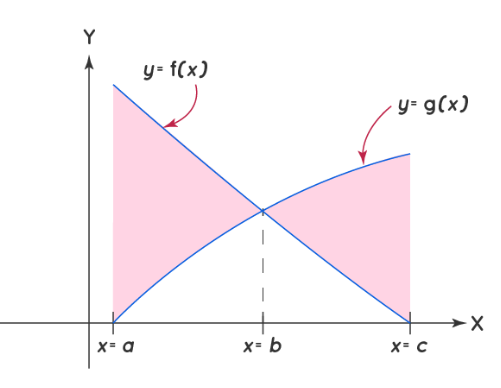
$\quad$
Standard Areas:
-
Area bounded by two parabolas $\mathrm{y}^2=4 \mathrm{ax}$ and $\mathrm{x}^2 =4 \mathrm{by}$; $\mathrm{a}>0, \mathrm{~b}>0$ : $$ A =\frac{16 \mathrm{ab}}{3} $$
-
Area bounded by Parabola $y^2=4 a x$ and Line $y=m x$: $$ A =\frac{8 a^2}{3 m^3} $$
-
Area of an Ellipse $\frac{\mathrm{x}^2}{\mathrm{a}^2}+\frac{\mathrm{y}^2}{\mathrm{~b}^2}=1$ : $$ A=\pi \mathrm{ab} $$






