यूनिट 1 सटीक अवस्था

हमारे पहले अध्ययन से हम जानते हैं कि तरल और गैस ऊष्मीय कहे जाते हैं क्योंकि वे प्रवाह के कारण योग्य होते हैं। दोनों अवस्थाओं में तरलता का कारण यह है कि कणों को आसानी से चलने की क्षमता होती है। इसके विपरीत, ठोसों में अवयवी अणुओं के स्थानिक स्थान होते हैं और केवल अपने औसत स्थानों के बारे में हलके संख्यत्मा अंतर्राल पर दबाव बना सकते हैं। यह ठोस में कठिनता का खास कारण है। ये गुण अवयवी अणुओं की प्रकृति और उनके बीच मोज़ून करने वाले बंधनीय बलों पर निर्भर करते हैं। संरचना और गुणों के बीच संबंध नए सटीक सामग्री की खोज में मदद करता है। उदाहरण के लिए, कार्बन नैनोट्यूब नया सामग्री है जिसमें स्टील से मजबूत, एल्युमिनियम से हल्का और तांत्रिकीय गुण से काठ के प्रदान करने की क्षमता होती है। ऐसी सामग्री सामग्री और समाज के भविष्य में विकास में एक विस्तार भूमिका निभा सकती है। अन्य कुछ सामग्री जिन्हें भविष्य में महत्वपूर्ण भूमिका निभाने की उम्मीद हैं, उच्च तापमान अधिष्ठान, चुंबकीय सामग्री, पैकेजिंग के लिए जैविक र्पुमर, शल्य निर्माण में जैविक राशियाँ, आदि हैं। इसप्रकार, इस स्थिति का अध्ययन वर्तमान परिदृश्य में और अधिक महत्वपूर्ण हो जाता है।

इस यूनिट में, हम अणुओं के विभिन्न संभावित व्यवस्थाओं पर चर्चा करेंगे जो कि ठोसों के विभिन्न गुणों को प्रदान करने में भिन्न प्रकृति की वजह से होती हैं। हम यह भी सीखेंगे कि ये गुण संरचनात्मक अविन्यास या न्यूनतम मात्रा में अविशुद्धियों के मौजूद होने के कारण कैसे संशोधित हो जाते हैं।

1.1 सटीक अवस्था की सामान्य विशेषताएं

कक्षा XI में आपने सीखा है कि पदार्थ तीन अवस्थाओं में मौजूद हो सकते हैं, अर्थात ठोस, तरल और गैस। एक दिए गए तापमान और दबाव की स्थितियों के तहत, किस धातु की कौन सी सटीक अवस्था सबसे स्थायी होगी इस पर दो प्रतिविरोधी कारकों का अवलोकन करना। ये मेंले बनाने वाले बालों के अंतरअणुगत मांग ताकतें होती हैं जो कि कणों (या परमाणुओं या आयों) को एक दूसरे के नजदीक रखने की प्रवृत्ति रखती हैं और ऊष्मीय को केवल उन्हें तेजी से अलग रखने के लिए बनाती हैं। पर्याप्त कम तापमान पर, ऊष्मीय शक्ति कम होती है और अंतरअणुगत मांगें इतने पास आती हैं कि वे एक-दूसरे को चिपकने लगती हैं और स्थान लेती हैं। ये अपनी औसत स्थानों के चारों ओर हल्के संख्यत्मा अंतराल में फिर भी हिल सकती हैं और पदार्थ सटीक अवस्था में मौजूद होते हैं।

सटीक अवस्था की निम्न विशेषताएं हैं:

• (i) उनका निर्दिष्ट भार, ठोस, और आकार होता है।
• (ii) अंतरअणु दूरियां कम होती हैं।
• (iii) अंतरअणु शक्तियां मजबूत होती हैं।
• (iv) इनके घटक कण (परमाणु, अणु या आयों) नियतित स्थानों में होते हैं और केवल उनके औसत स्थानों के बारे में हल्के संख्यत्मा अंतर्राल में दबाव बना सकते हैं।
• (v) वे अअकोंप्रेसिबल और कठिन होती हैं।

1.2 अनियामित और क्रिस्टलीय सटीक

सॉलिड को उनके घटक कणों के व्यवस्था के क्रम के आधार पर क्रिस्टलीय या असंरचनात्मक रूप में वर्गीकृत किया जा सकता है। एक क्रिस्टलीय ठोस आमतौर पर एक बड़ी संख्या के छोटे-छोटे क्रिस्टलों से मिलकर बना होता है, प्रत्येक क्रिस्टल में एक निश्चित विशेष ज्यामिति आकार होता है। क्रिस्टल में तत्वीय कणों (परमाणु, अणुओं या आयों) की व्यवस्था क्रमशः और निरंतर तीन आयामों में होती है। यदि हम क्रिस्टल के एक क्षेत्र में पैटर्न का अवलोकन करें, तो हम स्थानों की समस्या से बहुत दूर हो सकती हैं तो सत्यापित कर सकते हैं कि केवल निरीक्षण स्थान से कितनी दूर हो रहे हों केवल धातुओं की स्थिति को भलीभांति अनुमानित किया जा सकता है। इस प्रकार, क्रिस्टल में एक लंबा क्रम क्रम जो इसका अर्थ होता है कि यहाँ धातुओं की व्यवस्था की एक नियमित पैटर्न होती है जो पूरे क्रिस्टल पर नियमित रूप से पुन: प्राप्त होती है। सोडियम क्लोराइड और क्वार्ट्ज़ क्रिस्टलीय ठोस के प्रमुख उदाहरण हैं। कांच, रबर और कई प्लास्टिक ठोस जब उनकी तरल ठंड के समय जमते हैं, उनमें संरचनाएं नहीं बनती हैं। इन्हें असंरचित ठोस कहा जाता है। “असंरचित” शब्द ग्रीक शब्द अमोर्फॉस से आया है, जिसका अर्थ होता है कि कोई आकार नहीं है। ऐसे एक ठोस में घटक कणों (परमाणु, अणुओं या आयों) की व्यवस्था में केवल कम दूरी क्रम होता है। इस एवरीनमेंट में, एक नियमित और नियमित रूप से पुन: प्रतिध्वनित पैटर्न केवल छोटी दूरियों में देखा जाता है। नियमित पैटर्न बिखर जाते हैं और बीच में व्यवस्था असंगत होती है। क्योंकि द्रव में तत्वीय कणों की व्यवस्था में अंतर होता है, इन दो प्रकार के ठोस में उनकी गुणों में अंतर होता है।

क्रिस्टलीय ठोसों में सट्टा मिलता है। किसी विशिष्ट तापमान पर वे धीरेधीरे पिघलते हैं और तरल हो जाते हैं। दूसरी ओर, असंरचित ठोस में संतृप्त होने पर क्ठोस पिघलते हैं, तरल होते हैं और तापमान के एक सीमा में बह होते हैं और विभिन्न आकारों में मोल्ड किए जा सकते हैं। असंरचित ठोसों की संरचनाएँ द्रव की तरह होती हैं। क्योंकि तत्वीय कणों की व्यवस्था में अंतर होने के कारण, दोनों प्रकार के ठोस में उनकी संरचना में अंतर होता है।

क्रिस्टलीय ठोसों में एक तीव्र पिघलने का स्थान होता है। एक विशेष तापमान पर वे एक बार मेल्ट हो जाते हैं और तरल हो जाते हैं। जबकि, असंरचित ठोस में संतृप्त होने पर कस्ठोस नरम हो जाते हैं, पिघलते हैं और तरल और विभिन्न तापमान की सीमा में बहाने लगते हैं और विभिन्न आकारों में मोल्ड हो सकते हैं। असंरचित ठोस की संरचना में द्रव की तरहीनता होती है। वे हालांकि धीरे-धीरे बहते हैं। इसलिए, कभी-कभी इन्हें खुद स्थानिकी ठोस या सुपर कूल्ड द्रव कहा जाता है।

लवणीय तत्वों के सभी धातु, तत्वीय हलके और हल्के गैस धातु मिश्रित वर्ग के सभी द्रव्य में मध्यमी या बहुसमबाधी स्वरूप माध्यम हैं, यहाँ तक कि कठिन तथा द्रवियों के अन्तरलिपि भार और फंसाव की धारणा के समय ही ई-द्रवावलंबी हो जाती है। दैर्घ्यमापी सुत्र और वायवीय सगम संवेदनशीलता की पहचान भी समस्त दिशाओं में समान हो जाती है। यह उनके लंबे-समानिक अव्यवस्था और सभी दिशाओं में निश्चित अवश्या नहीं होती है, इसलिए समस्त व्यवस्था समान मान जाती है। इस प्रकार, किसी भी भौतिक गुण की मूल्य किसी भी दिशा के उसी रूप में होगी।

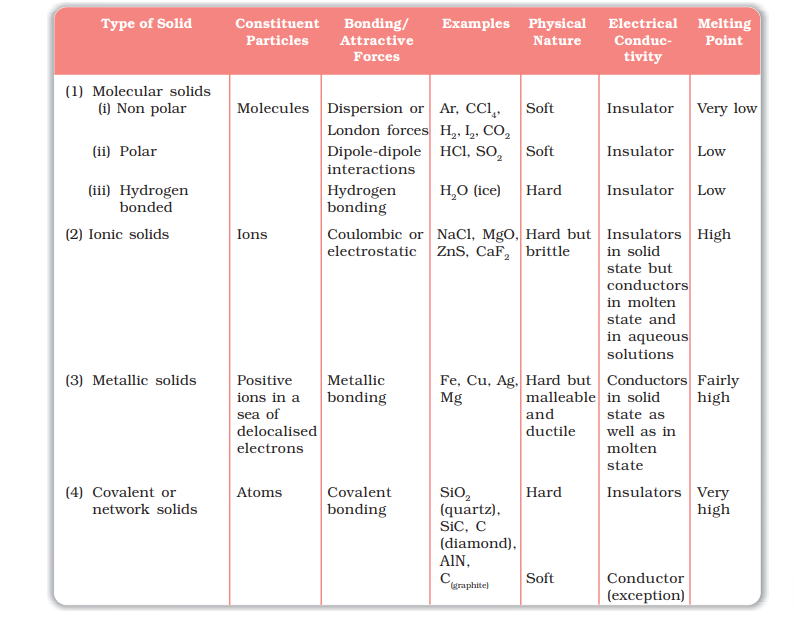
क्रिस्टलीय ठोस पदार्थों को विभिन्न तरीकों में वर्गीकृत किया जा सकता है। विधि उद्देश्य पर निर्भर करती है। यहां, हम संरचक अणुओं को संयुक्त तत्वांशों को साझा करने वाले बहुआभासी तारंगबल या बंध द्वारा क्रिस्टलीय ठोसों का वर्गीकरण करेंगे। इनमें शामिल हैं - (i) वान दे वालस बल; (ii) आयोनी बंध; (iii) सहभाजी बंध; और (iv) धातुवीय बंध। इस आधार पर, क्रिस्टलीय ठोस को चार श्रेणियों में वर्गीकृत किया जाता है, जैसे आणविक, पारदर्शी, धातुवीय और सहभाजी ठोस। आइए अब हम इन श्रेणियों के बारे में सीखें।

1.3.1 आणविक ठोस

मोलेक्यूल आणव ही आणविक ठोस के संरचक तत्व होते हैं। ये निम्नांकित श्रेणियों में और विभाजित होते हैं:

(i) अपोलर आणविक ठोस: इसमें अथवा कोई अपोलर सहभाजी बंधों द्वारा बने गए मोलेक्यूल हैं, उदाहरण के लिए, अर्गन और हीलियम, अथवा उदाहरण के लिए, H2, Cl2 और I2। इन ठोस पदार्थों में, परम प्रभाव बलों या लंदन बलों द्वारा आणव या मोलेक्यूलों को बांधा जाता है, जिसके बारे में आपने 11 वीं कक्षा में सीखा है। ये पदार्थ नरम होते हैं और बिजली के अच्छे प्रवाहक नहीं होते हैं। इनका पिघलने का अंक नीचा होता है और आमतौर पर कमरे की तापमान और दबाव पर तरल या गैसी होते हैं।

(ii) पोलर आणविक ठोस: जैसे HCl, SO2 इत्यादि जैसे पदार्थों के मोलेक्यूल धातुवीय बंधों द्वारा बने होते हैं। इस तरह के ठोसों में मोलेक्यूलों को एक दूसरे के साथ अपेक्षाकृत मजबूत द्विपोली-द्विपोली प्रभावों द्वारा जोड़ा जाता है। ये पदार्थ नरम होते हैं और बिजली के अच्छे प्रवाहक नहीं होते हैं। इनका पिघलने का संकेत अपोलर आणविक ठोसों की तुलना में ऊंचा होता है, फिर भी इनमें से बहुत से ठोस गैसों या तरल पदार्थों में होते हैं, सामान्य तापमान और दबाव पर। सॉलिड SO2 और सॉलिड NH3 इन ठोसों के कुछ उदाहरण हैं।

(iii) हाइड्रोजन बंधित आणविक ठोस: इस तरह की ठोसों के मोलेक्यूल में H और F, O या N अणुओं के बीच पोलर धातुवीय बंध होते हैं। तर्कसंगत हाइड्रोजन बंधित मोलेक्यूलों को जैसे H2O (बर्फ) आदि के मोलेक्यूलों के साथ बाँधा है। इनका बिजली का चालक नहीं होता है। आमतौर पर इनके रूम तापमान और दबाव पर थोड़े से ठोस या तरल होते हैं।

1.3.2 आयोनी ठोस

आयोन आयोनी ठोस के संरचक तत्व होते हैं। इस तरह के ठोस तीन-आयामी व्यवस्थाओं द्वारा लगातार (इलेक्ट्रोस्टेटिक) बलों द्वारा बने होते हैं। ये पदार्थ सौष्ठविक और नाजुक होते हैं। इनका पिघलने और उबलने एक अंक कई उच्च होता है। क्योंकि आयोंस मुक्त तत्व घूमने के लिए मुक्त नहीं होते हैं, इसलिए वे ठोस अवस्था में विद्युतचालक होते हैं। हालांकि, पिघले हुए अवस्था या पानी में योग में, आयोंस घूमने में मुक्त हो जाते हैं और वे बिजली चालित करते हैं।

1.3.3 धातुवीय ठोस

मेटल ऐटम के पॉजिटिव आयनों के संग्रह को चक्रवाती इलेक्ट्रॉनों द्वारा घेरा गया है और एकजुट है। ये इलेक्ट्रॉन मोबाइल हैं और क्रिस्टल के अंदर अगल-अगल बिखरे हुए हैं। प्रत्येक मेटल ऐटम इलेक्ट्रॉन को इस मोबाइल इलेक्ट्रॉनों के संग्रह में एक या अधिक इलेक्ट्रॉनों का योगदान करता है। ये मुक्त और मोबाइल इलेक्ट्रॉन मेटल की उच्च विद्युतीय और तापीय प्रवाहशीलता के ज़िमेदार हैं। जब एक विद्युतीय क्षेत्र लागू होता है, तो ये इलेक्ट्रॉन पॉजिटिव आयनों के नेटवर्क के माध्यम से प्रवाहित होते हैं। उसी प्रकार, जब धातु के एक भाग में गर्मी सप्लाई की जाती है, तो स्थानिक ऊष्मीय ऊर्जा मुक्त इलेक्ट्रॉनों द्वारा सभी प्रांतों में विस्तारित की जाती है। मेटल की एक और महत्वपूर्ण विशेषता उनकी चमक और रंग है। यह भी उनमें मुक्त इलेक्ट्रॉनों की मौजूदगी के कारण होता है। मेटल अत्यधिक मालेशियों और मिले हुए होते हैं।

1.3.4 कोवलेंट या नेटवर्क ठोस

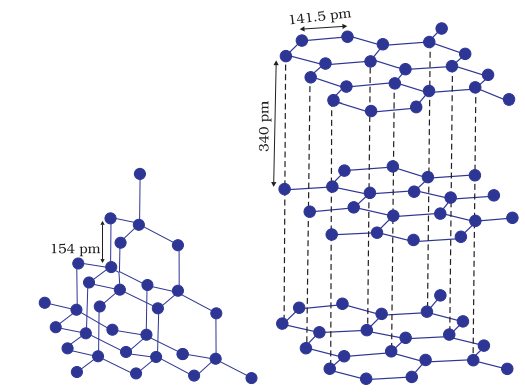
अर्क-मेटल के सृजन से निर्मित गैर-मेटलों की विविध ठोस वास्तुओं में दयानुसार आटमों के बीच कोवलेंट बंध बनती है। ये भी विशाल मोलेक्युल कहलाती हैं। कोवलेंट बंध सकारात्मक और दिशानिर्देशी होते हैं, इसलिए आणु अपनी स्थिति पर बहुत मजबूती से बंद होतें हैं। ऐसे ठोस ठोस बहुत कठोर और नाजुक होते हैं। उनका गरम होने का बिंदु अत्यधिक होता है और घिघरने से पहले वे तोड़ सकते हैं। वे बिजाली कन्डक्टर नहीं होते हैं और विद्युत प्रवाह नहीं करते हैं। डायमंड (चित्र 1.3) और सिलिकॉन कार्बाइड इस प्रकार की ठोसों के उदाहरण हैं। हालांकि ग्रेफाइट (चित्र 1.4) भी इस वर्ग के क्रिस्टलों में शामिल होता है, लेकिन यह मुलायम होता है और विद्युत का चालक होता है। इसकी असाधारण गुणवत्ताएं इसके विशिष्ट संरचना के कारण होती हैं। कार्बन आणु अलग-अलग परतों में व्यवस्थित होते हैं और प्रत्येक कार्बन आणु इसी परत में उसके पड़ोसी आणुओं के साथ कोवेलेंट बंधित होता है। प्रत्येक आणु का चौथा वैलन्स इलेक्ट्रॉन अलग-अलग परतों के बीच मौजूद होता है और आसानी से चलने वाला होता है। इन मुक्त इलेक्ट्रॉनों के कारण ग्रेफाइट एक अच्छा विद्युत कन्डक्टर होता है। विभिन्न परतें एक दूसरे पर स्लाइड कर सकती हैं। इसलिए ग्रेफाइट एक मुलायम ठोस और अच्छा ठोस स्नेहक होता है।

इनटेक्स्ट प्रश्न

1.5 इनके आधार पर अलग-अलग श्रेणियों में निम्नलिखित ठोसों को वर्गीकृत करें: पोटेशियम सल्फेट, टिन, बेंजीन, यूरिया, अन्निया, पानी, जस्ता सल्फाइड, ग्रेफाइट, रूबिडियम, आर्गन, सिलिकॉन कार्बाइड।

1.6 ठोस A ठोस रूप में और घले हुए अवस्था में बहुत कठोर बिजली इंसुलेटर है और बहुत उच्च तापमान पर पिघलता है। यह ऐसा किस प्रकार का ठोस है?

1.7 आयक ठोस स्नेही अवस्था में बिजली प्रवाह करते हैं, लेकिन ठोस अवस्था में नहीं। व्याख्या करें.

1.8 कौन से ठोसों के माध्यम से विद्युत प्रवाह किया जा सकता है, मुलायम हैं और मल्लेशियों और मिले हुए हैं?

1.4 क्रिस्टल जाल और इकाई कण

तुम्हें जरूर ध्यान आया होगा कि जब टाइल्स को फ्लोर को ढँकने के लिए रखा जाता है, तो एक बार फिराया गया पैटर्न उत्पन्न होता है। अगर हम फ्लोर पर टाइल्स रखने के बाद टाइल्स के सभी स्थानों पर एक ही स्थान मार्क करें (जैसे कि टाइल का केंद्र), और केवल मार्क किए गए स्थानों को ध्यान में रखें, तो हमें एक सेट के रूप में स्थानों का संचय मिलता है। यह सेट के स्थानों का स्‍कैफफोल्‍डिंग है, जिस पर टाइल रखकर पैटर्न विकसित किया गया है। यह स्कैफफोल्डिंग एक स्पेस लैटिस है, जिस पर दो-आयामी पैटर्न स्थानिक इकाइयों को लगाकर विकसित होता है।

संरचनात्मक इकाई को मूल या मोटीफ भी कहा जाता है। जब मोटीफ प्रतिष्ठित स्थानों पर स्थान लैटिस में रखे जाते हैं, तो एक पैटर्न उत्पन्न होता है। क्रिस्टल संरचना में, मोटीफ एक अणु, परमाणु या आयन होता है। एक स्थान लैटिस, जिसे क्रिस्टल लैटिस भी कहा जाता है, ये मोटीफ के स्थानों की स्थानिकता का पैटर्न है। दूसरे शब्दों में, स्थान लैटिस एक अमूर्त स्कैफफोल्डिंग है क्रिस्टल संरचना के लिए। जब हम स्थान लैटिस के स्थानों पर मोटीफ को एक एकार्यप्रद तरीके से रखते हैं, तो हमें क्रिस्टल संरचना प्राप्त होती है। चित्र 1.5 में एक मोटीफ, दो-आयामी लैटिस और एक काल्पनिक दो-आयामी क्रिस्टल संरचना दिखाई गई है, जो दो-आयामी लैटिस में मोटीफ को रखकर प्राप्त होती है।

स्थान लैटिस की आयामिति स्थानों के विभिन्न प्रकारों का उत्पन्न होती है। चित्र 1.6 में दो भिन्न लैटिस में स्थानों की व्यवस्था दिखाई गई है। क्रिस्टलीय कठोर पदार्थों के मामले में, स्थान लैटिस एक तीन-आयामी सरणी होती है जो स्थानिकतात्मक मोटीफ्स को जोड़ती है। प्रतिस्थिति का प्रतिष्ठान। प्रतिलिपित आधार या मोटीफ की संरचना समान होती है और क्रिस्टल में प्रत्येक एक में समान होती है, केवल सतह पर अलग है।

क्रिस्टल लैटिस के निम्नलिखित विशेषताएँ हैं: (a) लैटिस में प्रत्येक बिंदु को लैटिस बिंदु या लैटिस स्थान कहा जाता है। (b) क्रिस्टल लैटिस में प्रत्येक बिंदु में एक यौगिक अथवा अणु किसी एक संरचनात्मक कण होता है, जो एक परमाणु, एक मोलेक्यूल (अणुओं का समूह) या एक आयन हो सकता है। (c) लैटिस ज्यामिति को प्रकाशित करने के लिए सीधी रेखाएं लैटिस बिंदुओं को जोड़ती हैं।

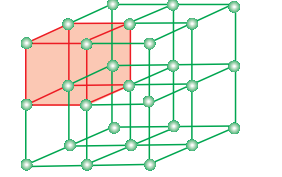
क्रिस्टल की पूर्णता को संदर्भित करने के लिए क्रिस्टल के स्थान लैटिस का छोटा सा हिस्सा ही काम में लाया जाता है। इस छोटे से हिस्से को इकाई कक्ष कहा जाता है। इकाई कक्ष को कई तरीकों से चुना जा सकता है। सामान्यतः वह कक्ष चुनी जाती है जिसमें सबसे छोटी चौड़ी और एक साथी पक्षों की लम्बाई होती है और तीन आयामों में इकाई कक्ष को स्थानांतरणीय विस्तार द्वारा पूरा किया जा सकता है। चित्र 1.7 में दो-आयामी लैटिस की इकाई कक्ष के चलते पूरे क्रिस्टल संरचना का आनंद उठाने के लिए इकाई कक्ष का चलता हुआ दिखाया गया है। इसके अलावा, इकाई कक्षों की आकृतियां ऐसी होती हैं कि इनको खाली जगह छोड़े बिना पूरा लैटिस भर सकती हैं।

दो आयामों में एक समरेखायुक्त चौखंबा जिसके पक्षों की लंबाई ‘ए’ और ‘बी’ है और इन पक्षों के बीच का कोण ‘र’ है, यह इकाई कक्ष के रूप में चुना जाता है। दो-आयामी में संभावित इकाई कक्ष चित्र 1.8 में दिखाई गई हैं।

त्रिआयामी क्रिस्टल संरचना में, यूनिट सेल निम्नलिखित के द्वारा विशेषित होती है:

त्रिआयामी क्रिस्टल जाली और उसके यूनिट सेल का एक हिस्सा चित्र 1.9 में दिखाया गया है।

त्रिआयामी क्रिस्टल संरचना में, यूनिट सेल निम्नलिखित द्वारा विशेषित है:

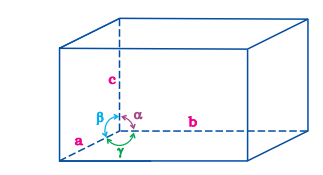
(i) तीन संपूर्ण मुद्रा a, b और c के अलावा उसकी आयाम। इन पक्षों के मध्य कोण हो सकतें हैं या हो सकती हैं।

(ii) पक्षों के बीच कोण, a (b और c के बीच), b (a और c के बीच) और g (a और b के बीच)। इस प्रकार, एक यूनिट सेल छह पैरामीटर a, b, c, a , b और g द्वारा विशेषित होती है। एक साधारण यूनिट सेल के इन पैरामीटर चित्र 1.6 में दिखाए गए हैं।

1.4.1 प्राथमिक और केंद्रित यूनिट सेल

यूनिट सेल को व्यापक रूप से दो श्रेणियों में विभाजित किया जा सकता है, प्राथमिक और केंद्रित यूनिट सेल।

(a) प्राथमिक यूनिट सेल: जब तत्व पदार्थ केवल यूनिट सेल के कोनों पर मौजूद होते हैं, तो उसे प्राथमिक यूनिट सेल कहा जाता है।

(b) केंद्रित यूनिट सेल: जब एक यूनिट सेल में कोनों के अलावा किसी अन्य स्थान पर एक या अधिक तत्व पदार्थ मौजूद होते हैं, तो उसे केंद्रित यूनिट सेल कहा जाता है। केंद्रित यूनिट सेल तीन प्रकार की होती है:

(i) केंद्रित शरीर यूनिट सेल: इस यूनिट सेल में एक तत्व पदार्थ (परमाणु, अणु या आयन) उसकी दिशाभूमि के मध्य में होता है जो कि कोनों पर मौजूद होते हैं।

(ii) मुख-केंद्रित यूनिट सेल: इस यूनिट सेल में प्रत्येक भुजा के बीच मध्य में एक तत्व पदार्थ मौजूद होता है, जो कि कोनों पर मौजूद होते हैं।

(iii) अंत-केंद्रित यूनिट सेल: इस यूनिट सेल में, दो विपरीत मुखों के मध्य एक तत्व पदार्थ मौजूद होता है, जो कि कोनों पर मौजूद होते हैं।

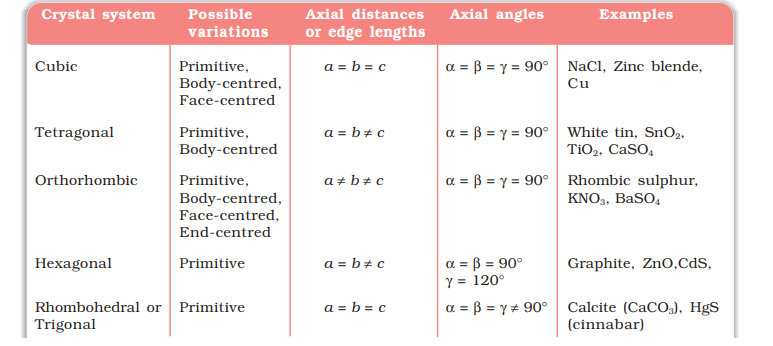
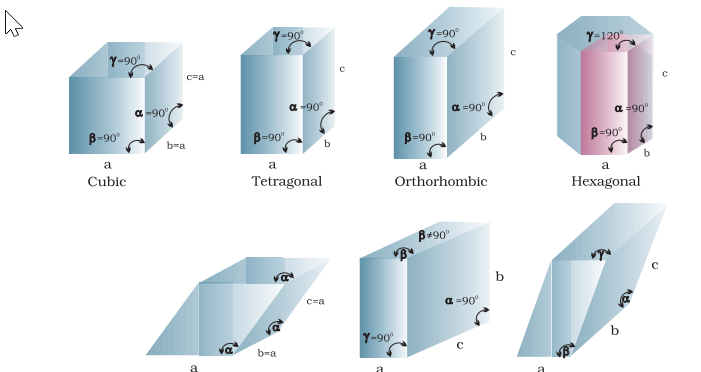
विविध क्रिस्टल की जांच से सिद्ध होता है कि उनमें से हर एक एक सात नियमित आकृतियों के अनुरूप माना जा सकता है। इन मूल नियमित आकृतियों को सात क्रिस्टल प्रणाली कहा जाता है। एक दिए गए क्रिस्टल का क्रिस्टल प्रणाली सिस्टम कितने कोणों के बीच की माप की जाती है और यह निर्धारित किया जाता है कि इसकी आकार की प्रमुख विशेषताओं को परिभाषित करने के लिए कितने धुरियों की जरूरत होती है। चित्र 1.11 में सात क्रिस्टल प्रणालियों को दिखाता है।

एक फ्रेंच गणितज्ञ, ब्रावेस, ने दिखाया है कि केवल 14 संभावित त्रिआयामी जाल होते हैं। इन्हें ब्रावेस जाल कहा जाता है। इन जालों की यूनिट सेलें निम्नलिखित बॉक्स में दिखाई गई हैं। इनके प्राथमिक यूनिट सेलों की विशेषताएं साथ ही उन केंद्रित यूनिट सेलों को भी दिया गया है जिन्हें वे बना सकते हैं, उन्हें तालिका 1.3 में सूचीबद्ध किया गया है।

1.5 यूनिट सेल में अणु की संख्या

हम जानते हैं कि कोई भी क्रिस्टल जाली बहुत बड़ी संख्या में यूनिट सेलों से बनी होती है और प्रत्येक जाली बिंदु द्वारा एक तत्व पदार्थ (अणु, अणु या आयन) आपूर्ति की जाती है। हम अब यह निकालें कि प्रत्येक पदार्थ का कौन सा हिस्सा एक विशेष यूनिट सेल का होता है।

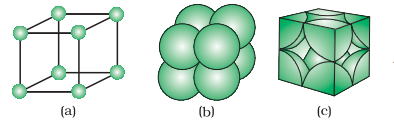
हम तीन प्रकार की घन इकाई कक्षाएं विचार करेंगे और सरलता के लिए मान लेंगे कि संघटक कण एक परमाणु है।

प्राथमिक घन इकाई कक्ष में केवल कोने पर एटम होते हैं। प्रत्‍येक कोने पर एक एटम उसके आस-पास के आठ संचालनकोणीय इकाइयों के बीच साझा किया जाता है, जैसा कि चित्र 1.12 में दिखाया गया है। एक ही सतह पर चार इकाइयाँ और ऊपरी (या निचली) पर चार इकाइयाँ शामिल हैं। इसलिए, केवल 1 8 वाँ हिस्सा एक विशेष इकाइ में वास्तव में एक एटम (या मोलेक्यूल या आयन) का होता है। चित्र 1.13 में, एक प्राथमिक घन इकाई कक्ष को तीन अलग-अलग तरीकों से चित्रित किया गया है। चित्र 1.13(a) में हर छोटा गोला केवल उस स्थान के आपत्तिजनक आकार में स्थित इधर की जगह की धमनी का प्रतिनिधित्व करता है और अपने वास्तविक आकार का नहीं। ऐसी संरचनाओं को खुली संरचनाएँ कहा जाता है। इधर की प्रतिष्ठानों का व्यवस्थान खुली संरचनाओं में आसानी से किया जा सकता है। चित्र 1.13 (बी) में एकांत वापरी मॉडल का चित्रण किया गया है जिसमें वास्तविक कण का आकार है और चित्र 1.13 (सी) में एक घन इकाई कक्ष में मौजूद विभिन्न एटमों के वास्तविक हिस्से दिखाए गए हैं।

सार्वभौमिक रूप से, क्योंकि प्रत्येक घन इकाई कक्ष में 8 एटम कोनों पर होते हैं, एक इकाई कक्ष में एक एटम की कुल संख्या 8 × 1/8 = 1 होती है।

1.5.2 शरीर-केंद्रित घन इकाई कक्ष

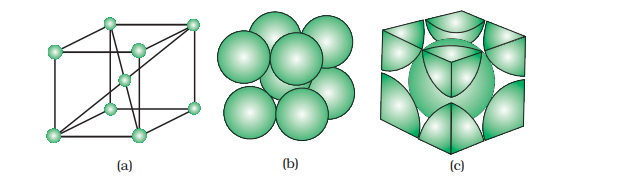
एक शरीर-केंद्रित घन इकाई कक्ष में प्रत्येक कोने पर एक एटम और उसके शरीर के केंद्र में भी एक एटम होता है। चित्र 1.14 (ए) खुली संरचना (बी) स्थान-भरण मॉडल और (सी) इकाई कक्ष जिसमें वास्तविक रूप से उसमें शामिल एटम के हिस्से दिखाए गए हैं इसका वर्णन करता है। ऐसा देखा जा सकता है कि केंद्रीय स्थान पर एटम उस इकाई कक्ष में पूर्णतः शामिल होता है जिसमें वह हाजिर होता है। इस प्रकार, एक शरीर-केंद्रित घन इकाई कक्ष में:

(i) 8 कोनों × 1/8 कोने के एटम = 8 × 1/8 = 1 एटम

(ii) 1 शरीर केंद्र एटम = 1 × 1 = 1 एटम \ इकाई कक्ष प्रति एटम की कुल संख्या = 2 एटम

1.5.3 मुख-केंद्रित घन इकाई कक्ष

एक मुख-केंद्रित घन इकाई कक्ष में घाटों पर सभी कोनों पर एटम होते हैं और क्यूब के सभी मुखों के केंद्र में होते हैं। चित्र 1.15 में यह देखा जा सकता है कि प्रतिष्ठान के केंद्र पर स्थित हर एटम दो समांतर इकाइयों के बीच साझा किया जाता है और प्रत्येक एटम का केवल 1/2 इकाई कक्ष में आता है। चित्र 1.16 में (अ) खुली संरचना (बी) स्थान-भरण मॉडल और (सी) इकाई कक्ष जिसमें वास्तविक रूप से उसमें शामिल एटम के हिस्से दिखाए गए हैं इसका वर्णन करता है। इस प्रकार, मुख-केंद्रित घन इकाई कक्ष में:

(i) 8 कोनों के एटम × 1/8 एटम प्रति इकाई कक्ष = 8 × 1/8 = 1 एटम

(ii) 6 मुख-केंद्रित एटम × 1/2 एटम प्रति इकाई कक्ष = 6 × 1/2 = 3 एटम

इकाई कक्ष प्रति एटम की कुल संख्या = 4 एटम

इनटेक्स्ट प्रश्न

1.9 ‘रेत्रिक का महत्व बताएं| 1.10 एक इकाई कक्ष का विशेषता संख्या बताएं 1.11 दो वस्तुओं को भेदित करें- (i) षट्-भुजीय और अर्ध-अन्तर्व्यासी इकाइयाँ (ii) मुख-केंद्रित और अंत-केंद्रित इकाइयाँ।

दक्षिण को 1.12 का हिस्सा समझाएं कि एक घाटी इकाई सेल के (i) कोने और (ii) शरीर केंद्र में केंद्र अणु का कितना हिस्सा उसकी प्रभावित पड़ाव इकाई सेल का होता है।

1.6 क्लोज़ पैकड संरचनाएँ

ठोस में, तत्विक कण पास-बस जाने के बाद, कम से कम खाली स्थान छोड़ देते हैं। हम संघी तत्विक कणों को समान ताकत हैंस्ताओं के रूप में मान सकते हैं और तीन चरणों में त्रिविमीय संरचना का निर्माण कर सकते हैं।

(ए) एक आयाम में क्लोज़ पैकिंग एक आयाम में क्लोज़ पैकिंग संरचना में कणों को व्यवस्थित करने का केवल एक तरीका होता है, जो कि उन्हें एक पंक्ति में व्यवस्थित करने और एक दूसरे को स्पर्श करने का होता है (चित्र 1.17)।

इस व्यवस्था में, प्रत्येक कण अपने आसनी से बैठा है। एक कण के पास सबसे करीबी पडोसी का कुल अणु कहा जाता है। इस प्रकार, एक आयामी घट व्यवस्थान में कोऑर्डिनेशन अंक 2 होता है।

(बी) दो आयामों में क्लोज़ पैकिंग

बी-आयामी क्लोज़ पैकिंग संरचना को तीन हमदर्शीदार कणों के स्तंभन (स्थान) के माध्यम से उत्पन्न किया जा सकता है। इसे दो तरीकों से किया जा सकता है।

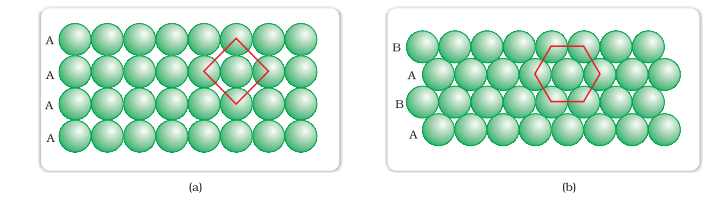
(i) द्वितीय पंक्ति पहली केसथ एक संपर्क में रखी जा सकती है जिसमें द्वितीय पंक्ति के कण पहली पंक्ति के कणों के ठीक ऊपर होते हैं। दो पंक्तियों के कणों को क्षैतिज और लंबवत रूप से संरेखित किया जाता है। यदि हम पहली पंक्ति को ‘ए’ प्रकार की पंक्ति कहें, तो द्वितीय पंक्ति पहली पंक्ति के बिल्कुल समान होने की वजह से, यह भी ‘ए’ प्रकार की होगी। इसी तरह, हम और पंक्तियाँ रखकर आगे की पंक्ति को प्राप्त कर सकते हैं जैसा कि चित्र 1.18 (ए) में दिखाया गया है।

इस व्यवस्था में, प्रत्येक कण अपने चार अपने पडोसियों से संपर्क में है। इस प्रकार, चतुर्भुज आयामी कोऑर्डिनेशन अंक 4 होता है। इस उच्चविमीय में, इन 4 छोटी प्रत्येक पडोसी कणों के केंद्रों को जोड़ा जाता है, तो एक वर्ग बनता है। इसलिए इस मंडल को दो आयाम में चोर क्लोज़ पैकिंग कहा जाता है।

(ii) दूसरी पंक्ति पहली पंक्ति के डिप्रेशन में फिट होने के लिए टेढ़े-मेढ़े ढंग से ऊपर रखी जा सकती है। अगर पहली पंक्ति में गोले की व्यवस्था को ‘ए’ प्रकार कहा जाता है, तो दूसरी पंक्ति में व्यवस्था अलग होती है और ‘बी’ प्रकार कही जा सकती है। जब तीसरी पंक्ति पहली पंक्ति के समक्ष टेढ़े-मेढ़े ढंग से स्थानांतरित की जाती है, तो उसके गोले पहली परत के गोलों के साथ मिलते हैं। इसलिए यह परत भी ‘ए’ प्रकार की होती है। ऐसी ही तरह चौथी पंक्ति के गोले दूसरी पंक्ति के गोलों के साथ मिलते हैं (‘बी’ प्रकार)। इसलिए यह व्यवस्था ABAB प्रकार की होती है। इस व्यवस्था में कम खाली जगह होती है और यह पैकिंग सावधानियों से अधिक कारगर होती है। प्रत्येक गोला अपने सभी पड़ोसियों से संपर्क में होता है और दो आयामी संबंध संख्या 6 होती है। इन छे गोलों के केंद्र एक नियमित षट्कोण के कोनों पर होते हैं (चित्र 1.18 बी) इसलिए इस पैकिंग को दो आयामी षट्कोणीय नजदीकियों की दो आयामी क्लोजपैकिंग कहा जाता है। चित्र 1.18 (बी) में दिखाया गया है कि इस परत में कुछ खाली जगहें (खाली स्थानें) होती हैं। ये त्रिकोणीय आकार की होती हैं। त्रिकोणीय खाली स्थानों को दो अलग-अलग प्रकार की कहा जाता है। एक पंक्ति में, त्रिकोणों के शीर्ष ऊपर की ओर होते हैं और उसकी अगली परत में नीचे की ओर होते हैं।

(ग) तीन आयामी नजदीकी में क्लोज पैकिंग

सभी वास्तविक संरचनाएं तीन आयामी संरचनाएं होती हैं। इन्हें एक-दूसरे के ऊपर डाले गए दो-आयामी परतों को इस्तेमाल करके प्राप्त किया जा सकता है। अगले खंड में, हमने दो आयामी में क्लोज पैकिंग की चर्चा की थी जो दो प्रकार हो सकता है; चौकोर नजदीकी और षट्कोणीय नजदीकी। चलो देखें कि इनसे क्या प्रकार की तीन आयामी नजदीकी क्लोज पैकिंग प्राप्त की जा सकती है।

(i) तीन आयामी क्लोज पैकिंग ने दो-आयामी चौकोर नजदीकी परतों को बनाया है: जब हम दूसरी चौकोर नजदीकी परत को पहली परत के ऊपर रखते हैं, तो हम वही नियम अपनाते हैं जो जब एक पंक्ति के समक्ष दूसरी पंक्ति रखी गई थी। दूसरी परत को पहली परत पर ऐसे रखा जाता है, जिसके परत के गोले उच्च स्तर के गोलों के साथ बिल्कुल अपेक्षित होते हैं। इस व्यवस्था में, दोनों परतों के गोले सही ढंग से आपस में आयताकार रूप से मिलते हैं जैसा कि चित्र 1.19 में दिखाया गया है। इसी तरह, हम और परतें एक-दूसरे के ऊपर रख सकते हैं। अगर पहली परत में गोलों की व्यवस्था को ‘ए’ प्रकार कहा जाता है, तो सभी परतों में वही व्यवस्था होती है। इस परतांकित यंत्र को सादा घन यंत्र कहा जाता है, और इसका यूनिट सेल पामानिक घन यूनिट सेल होता है (चित्र 1.19 देखें)।

(ii) दो आयामी षट्कोणीय नजदीकी से तीन आयामी क्लोज पैकिंग: तीन आयामी क्लोज पैकिंग संरचना को परतों को एक-दूसरे के ऊपर रख कर प्राप्त किया जाता है।

(अ) पहली परत को दूसरी परत के ऊपर रखने के लिए

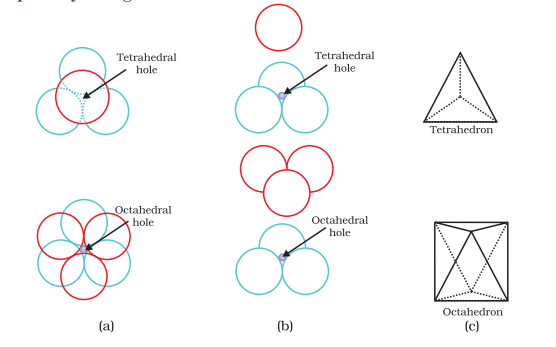
हम दो आयामी षट्कोणीय क्लोस पैक्ड स्तर ‘ए’ लेते हैं और उसके ऊपर एक समान स्तर रखते हैं जिसमें दूसरे स्तर के गोलाकार गोलाकारों को पहले स्तर के निष्कासनों में रखा जाता है। क्योंकि दोनों स्तरों के गोलाकार अलग-अलग होते हैं, इसलिए हम दूसरे स्तर को ‘बी’ के रूप में बुलाते हैं। चित्र 1.20 से यह देखा जा सकता है कि पहले स्तर के सभी त्रिकोणीय शून्यों को दूसरे स्तर के गोलाकारों से ढका नहीं जा सकता है। इससे विभिन्न व्यवस्थाओं को उत्पन्न किया जाता है। जहां दूसरे स्तर का गोलाकार पहले स्तर की शून्य के ऊपर होता है (या उल्टी) वहां एक त्रिकोणीय शून्य बना होता है। इन शून्यों को त्रिकोणीय शून्य कहा जाता है क्योंकि ये चार गोलाकारों के केंद्रों को जोड़ने पर एक त्रिकोणात्मक मिश्रण बनाते हैं। चित्र 1.20 में इन्हें ‘टी’ के रूप में चिह्नित किया गया है। चित्र 1.21 में एक ऐसी रिक्ति अलग से दिखाई गई है।

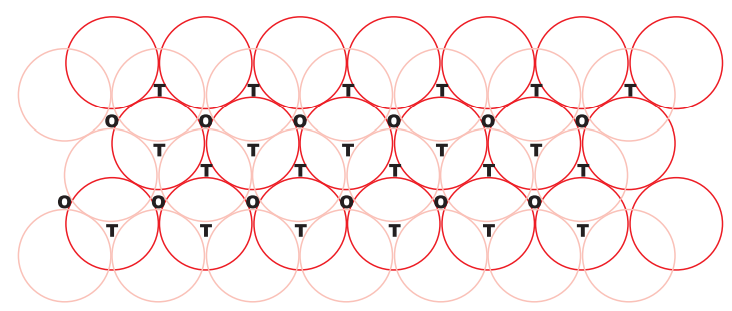
अन्य स्थानों पर, दूसरे स्तर में त्रिकोणीय रिक्तियां पहले स्तर की त्रिकोणीय रिक्तियों के ऊपर होती हैं, और इनकी त्रिकोणीय आकृतियों का आपस में कोई छिपकली नहीं होता। उनमें से एक त्रिभुज का शिर ऊपर की ओर होता है और दूसरा नीचे की ओर होता है। इन रिक्तियों को छह गोलाकारों द्वारा घेरा जाता है और इन्हें अक्टाहेद्राल शून्य कहा जाता है। चित्र 1.20 में इन्हें ‘ओ’ के रूप में चिह्नित किया गया है। चित्र 1.21 में एक ऐसी रिक्ति अलग से दिखाई गई है। इन दो प्रकार के शून्यों की संख्या सर्वधिकतम निकटतम गोलाकारों की संख्या पर निर्भर करती है।

तीसरे स्तर को दूसरे स्तर के ऊपर रखने पर दो संभावनाएं होती हैं।

(अ) त्रिकोणीय खाली जगहों को ढकना: दूसरे स्तर के त्रिकोणीय शून्यों को तीसरे स्तर के गोलाकारों से ढका जा सकता है। इस मामले में, तीसरे स्तर के गोलाकार सटीकता से पहले स्तर के गोलाकारों के साथ मिलते हैं। इस प्रकार, गोलाकारों का पैटर्न सुरक्षित किया जाता है। इस पैटर्न को अक्कड़ रूप में लिखा जाता है जैसे ABAB…. पैटर्न। इस संरचना को षट्कोणीय क्लोस पैक्ड (हेक्सीएसपी) संरचना कहा जाता है (चित्र 1.22)। इस तरह की पदार्थों की व्यवस्था में धातुओं जैसे मैग्नीशियम और जिंक पाए जाते हैं।

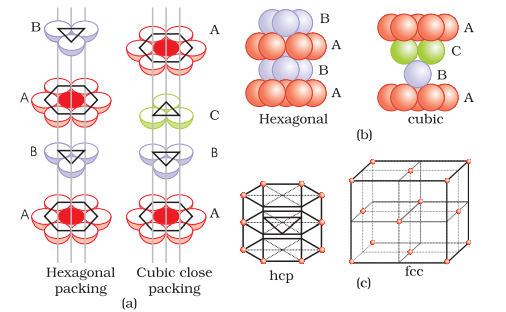
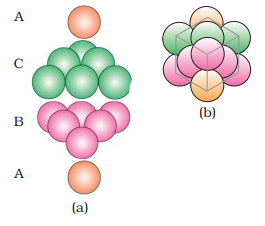
(ii) अक्टाहेद्राल खाली ढ़लानों को ढकना: तीसरी परत को एक ऐसे ढंग से दूसरी परत के ऊपर स्थापित किया जा सकता है कि इसके गोलाकार घेरों से अक्टाहेद्राल खाली ढ़लानें ढ़की जाएँ। इस ढंग से स्थापित किए जाने पर, तीसरी परत के गोलाकार घेरों को पहली या दूसरी परत के गोलाकार घेरों के साथ सामंजस्यित नहीं किया जाता है। इस व्यवस्था को ‘सी’ प्रकार कहा जाता है। केवल जब चौथी परत स्थापित की जाती है, तब इसके गोलाकार घेरे पहली परत के गोलाकार घेरों के सामंजस्यित होते हैं जैसा कि चित्र 1.22 और 1.23 में दिखाया गया है। इन परतों के पैटर्न को अक्सर ऐबीसीऐबीसी ……… के रूप में लिखा जाता है। यह संरचना साधारणतः सुंदरता पूर्ण क्लोज पैक्ड (सीसीपी) या चेहरा-केंद्रित घनीत (एफसीसी) संरचना कहलाती है। तांबा और चांदी जैसे धातुओं का ठोस मिश्रण इसी संरचना में क्रिस्टलीय होता है।

इन दोनों प्रकार की क्लोज पैकिंग अत्यधिक कुशल है और क्रिस्टल में 74% जगह भरी हुई होती है। इन दोनों में, हर गोलाकार घेरे 12 गोलाकार घेरों से संपर्क में होते हैं। इस प्रकार, संपर्क की संख्या इन दोनों संरचनाओं में 12 होती है।

1.6.1 यौगिक का सूत्र और भरे गए खाली ढ़लानों की संख्या

इस प्रकरण में पहले हमने सीखा है कि जब खण्ड पैकिंग से आत्मको करने से या हेक्टेगोनल क्लोज पैकिंग से आत्मको करने से तय द्विआयामी खाली ढ़लानें उत्पन्न होती हैं। कमीज्ञा ठोसों में, बड़े आयन (साधारणतः ऐनियन) क्लोज पैक्ड संरचना बनाते हैं और छोटे आयन (साधारणतः क्रियन) खाली ढ़लानों को कब्ज़ा करते हैं। अगर वायू आयन पर्याप्त छोटा है तो उसके आस-पास आयों परिभग पटिकाए जाते हैं, यदि बड़ा है, तो अक्टाहेद्राल खाली ढ़लानें पटिकाए जाते हैं। सभी अक्टाहेद्राल या तेत्राहेद्राल खाली ढ़लाने भरे नहीं जाते हैं। किसी दिए गए यौगिक में, भरे गए अक्टाहेद्राल या तेत्राहेद्राल खाली ढ़लानों का अंश यौगिक के रासायनिक सूत्र पर निर्भर करता है, जैसा कि निम्न उदाहरणों से देखा जा सकता है।

उदाहरण 1.1

दो तत्वों एक्स और वाई द्वारा एक यौगिक बनाई जाती है। तत्व वाई (ऐनियन के रूप में) सीसीपी बनाते हैं और तत्व एक्स (क्रियन के रूप में) सभी अक्टाहेद्राल खाली ढ़लानों को कब्जा करते हैं। यौगिक का सूत्र क्या है?

समाधान

वाई तत्व द्वारा सीसीपी जाल बनाया जाता है। उत्पन्न होनेवाले सभी अक्टाहेद्राल खाली ढ़लानें यौगिक के तत्वों की संख्या तक बराबर होंगी। क्योंकि तत्व एक्स के आवर्ती संख्या में सभी अक्टाहेद्राल खाली ढ़लानों का कब्ज़ा होता है, उनकी संख्या भी वाई तत्व के आवर्ती संख्या के बराबर होगी। इसलिए, तत्व एक्स और वाई के आवर्ती संख्याओं में सामान्य रूप से बराबर संख्याओं या 1:1 अनुपात में पाये जाने से, यौगिक का सूत्र XY होगा।

उदाहरण 1.2

तत्व बी के आणविक जाल का गठन होता है और तत्व ए के आणविक खाली ढ़लानों का 2/3 भरा जाता है। तत्व ए और बी द्वारा जो यौगिक बनाई जाती है, उसका सूत्र क्या होगा?

समाधान

उत्पन्�

त्रिकोणात्मक और अष्टकोण रिक्तियों का पता लगाना

हम जानते हैं कि संघटित संरचनाओं में त्रिकोणात्मक और अष्टकोण रिक्तियाँ होती हैं। हम ccp (या fcc) संरचना को लेते हैं और इन रिक्तियों को उसमें स्थान देते हैं।

(ए) त्रिकोणात्मक रिक्ति का पता लगाना

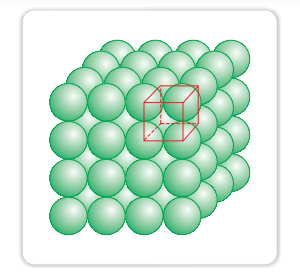
हम ccp या fcc जितीय लेटिस की एकक सेल को विचार करें [चित्र 1(a)]. इकाई सेल को आठ छोटे क्यूबों में विभाजित किया जाता है।

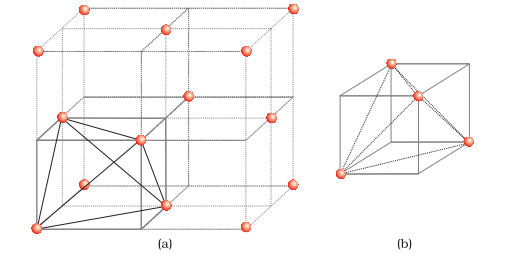
प्रत्येक छोटे क्यूब के विकर्ण पर एक एवम्‍ शामिल अणु होते हैं [चित्र 1(a)]। समस्त, प्रत्येक छोटे क्यूब में 4 अणु होते हैं। जब एक-दूसरे से जुड़े होते हैं, तो वह एक नियमित त्रिकोणाकार त्रिकोण बनाते हैं। इस प्रकार, प्रत्येक छोटे क्यूब में एक त्रिकोणात्मक रिक्ति होती है और कुल में आठ त्रिकोणात्मक रिक्तियां होती हैं। प्रत्येक आठ छोटे क्यूब में एक रिक्ति होती है एक ccp संरचना की एक इकाई सेल में। हम जानते हैं कि ccp संरचना में प्रति इकाई सेल 4 अणु होते हैं। इस प्रकार, त्रिकोणात्मक रिक्तियों की संख्या अणुओं की संख्या के दोगुनी होती है।

(ब) अष्टकोण रिक्ति का पता लगाना

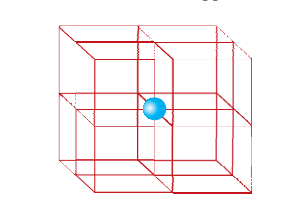
हम फिर से ccp या fcc जितीय लेटिस की एकक सेल को विचार करें [चित्र 2(a)]। क्यूब का शरीर मध्य में स्थित है, जो अवर्त है, लेकिन इसे छह अणुओं द्वारा घेरा गया है जो चेहरा केंद्रों पर स्थित हैं। यदि इन चेहरा केंद्रों को जोड़ा जाए, तो एक अष्टाकार उत्पन्न होता है। इस प्रकार, इस इकाई सेल में एक अष्टकोण रिक्ति क्यूब के शरीर के मध्य में होती है।

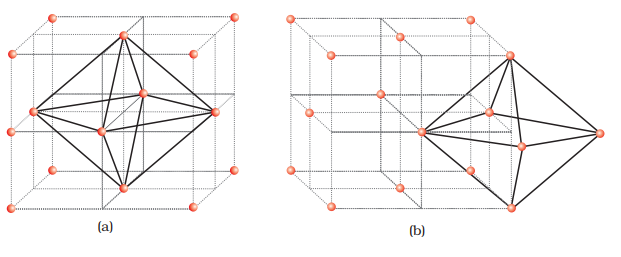
शरीर के साथ, हर एक 12 किनारों के बीच में एक-एक अष्टाकोण रिक्ति है [चित्र 2(b)]। यह छः अणुओं द्वारा घिरा होता है, इनमें से चार एक ही इकाई सेल (खोंजों पर 2 और चेहरे केंद्र पर 2) का होता है और दो आस-पास के इकाई सेलों के बेलोंग्स करता है। क्योंकि क्यूब के प्रत्येक किनारे को चार आस-पास के इकाई सेलों के बीच साझा किया जाता है, इस प्रकार उस पर स्थित अष्टाकोण रिक्ति भी होती है। प्रत्येक राइन का क्यूब चार आस-पास के इकाई सेलों में साझा की जाती है, इस प्रकार केवल 1/4 वांशिकता ही किसी विशेष इकाई सेल की होती है।

इस प्रकार घनी बंद संरचना में: क्यूब के शरीर केंद्र पर अष्टाकोण रिक्ति = 1 चार इकाई सेलों के बीच स्थित 12 अष्टाकोण रिक्तियां = 12 × 1/4 = 3

कुल अष्टाकोण रिक्तियों की संख्या = 4 हम जानते हैं कि ccp संरचना में प्रति इकाई सेल 4 अणु होते हैं। इस प्रकार, अष्टाकोण रिक्तियों की संख्या इस संख्या के बराबर होती है।

1.7 पैकिंग प्रभावशीलता

मुख्य संघटक अणु (अणु, अणुओं या आयन) जैसे भी पैक चिह्नों में हमेशा कुछ मुक्त जगह होती है। पैकिंग प्रभावशीलता वह प्रतिशत है जिसमें अणुओं द्वारा भरे गए कुल जगह की मात्रा होती है। आइए विभिन्न प्रकार की संरचनाओं में पैकिंग प्रभावशीलता की गणना करें।

1.7.1 एचसीपी और सीसीपी संरचनाओं में पैकिंग प्रभावशीलता

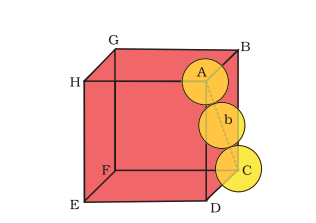
दोनों प्रकार की घनी बंद करना (एचसीपी और सीसीपी) समान रूप से प्रभावी होता है। हम सीसीपी संरचना में पैकिंग प्रभावशीलता की प्रभावशीलता गुणना करेंगे। चित्र 1.24 में साइन कक्ष रेखा ‘ए’ और चेहरा याय मान करें।

त्रिभुज $\triangle ABC$ में

$एसी^{2} या बिसी^{2}=एब^{2}+AB^{2}$

$=a^{2}+a^{2}=2 a^{2}$ या

$ए=\sqrt{2} ए$

यदि $र$ गोला का त्रिज्या है, तो हम पाएंगे

ए = 4र=√2ए

वांछित बाकी हमको नयी नहीं, or $a=\frac{4 \mathrm{r}}{\sqrt{2}}=2 \sqrt{2} \mathrm{r}$

(हम यह भी लिख सकते हैं, $\mathrm{r}=\frac{\mathrm{a}}{2 \sqrt{2}}$ )

हम जानते हैं, कि ccp संरचना में प्रत्येक यूनिट सेल के पूर्वाभासीत रूप में 4 गोलाकार होते हैं। चार गोलाकारों का कुल आयतन $4 \times(4 / 3) \pi r^{3}$ होता है और घन आयतन $\mathrm{a}^{3}$ या $(2 \sqrt{2} \mathrm{r})^{3}$ होता है।

इसलिए,

पैकिंग कुशलता $=\frac{\text { यूनिट सेल में चार गोलाकारों द्वारा आवर्तित आयतन } \times 100}{\text { यूनिट सेल का कुल आयतन }} $%

$$ \begin{aligned} & =\frac{4 \times(4 / 3) \pi r^{3} \times 100}{(2 \sqrt{2} r)^{3}} \text{\%} \end{aligned} $$ $$ \begin{aligned} & =\frac{(16 / 3) \pi r^{3} \times 100}{16 \sqrt{2} r^{3}} \text{\%} =74 \text{\%} \end{aligned} $$

1.7.2 पैकिंग कुशलता शरीर- केंद्रित घन संरचनाओं में

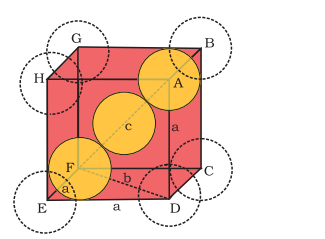
चित्र 1.25 से स्पष्ट होता है कि केंद्र के एटम को दो रेखाओं को छूना चाहिए जो एक दूसरे की विरोधी बाएं होती हैं।

$\triangle \mathrm{EFD}$ में,

$\mathrm{b}^{2}=\mathrm{a}^{2}+\mathrm{a}^{2}=2 \mathrm{a}^{2}$

$\mathrm{b}=\sqrt{2} \mathrm{a}$

अब $\triangle$ AFD में

$$ \begin{aligned} & c^{2}=a^{2}+b^{2}=a^{2}+2 a^{2}=3 a^{2} \ & c=\sqrt{3} a \end{aligned} $$

शरीरी रेखा की लंबाई $c$ के बराबर होती है $4 r$, जहां $r$ गोलाकार-सिफारिश (एटम) का त्रिज्या होता है, क्योंकि त्रिज्या वाले सभी तीन गोलाकार एक-दूसरे को छूते हैं।

इसलिए, $$\quad \sqrt{3} \mathrm{a}=4 \mathrm{r}$$ $$ \mathrm{a}=\frac{4 \mathrm{r}}{\sqrt{3}} $$

इसके अलावा हम लिख सकते हैं, $r=\frac{\sqrt{3}}{4} \mathrm{a}$

इस प्रकार की संरचना में, कुल अणु संख्या 2 होती है और उनके आयतन $2 \times\left(\frac{4}{3}\right) \pi \mathrm{r}^{3}$ होता है।

क्यूब का आयतन $\mathrm{a}^{3}$ के बराबर होगा $\left(\frac{4}{\sqrt{3}} \mathrm{r}\right)^{3}$ या $\mathrm{a}^{3}=\left(\frac{4}{\sqrt{3}} \mathrm{r}\right)^{3}$।

इसलिए,

पैकिंग कुशलता $=\frac{\text { यूनिट सेल में दो गोलाकारों द्वारा आवर्तित आयतन } \times 100}{\text { यूनिट सेल का कुल आयतन }} \text{\%}$

$$ \begin{aligned} & =\frac{2 \times(4 / 3) \pi r^{3} \times 100}{[(4 / \sqrt{3}) r]^{3}} \% \ & =\frac{(8 / 3) \pi r^{3} \times 100}{64 /(3 \sqrt{3}) r^{3}}=68 \text{\%} \end{aligned} $$

1.7.3 सादे क्युबिक जर्जर में पैकिंग कुशलता

सादे क्युबिक जर्जर में अणु केवल क्युब के कोनों पर स्थित होते हैं। कणों का प्रांत एक किनारा में संपर्क करता है (चित्र 1.26)।

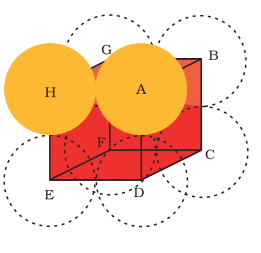
इस प्रकार, क्युब की किनारी या साइड $\mathrm{a}$, और प्रत्येक कण का त्रिज्या या अर्ध चौकों $\mathrm{r}$ के साथ सम्बंधित होते हैं

$$ \mathrm{a}=2 \mathrm{r} $$

घन यूनिट सेल का आयतन $=a^{3}=(2 r)^{3}=8 r^{3}$

एक सादे क्युबिक यूनिट सेल में केवल 1 एटम होता है

अवर्तित जगह का आयतन $=\frac{4}{3} \pi \mathrm{r}^{3}$

पैकिंग कुशलता

$\therefore$ पैकिंग कुशलता $$ \begin{gathered}

एक परमाणु की आयत आणविक संरचना के जिन्हें X-किरण विवरण से स्थापित किया जाता है, में कक्ष की भुजा “a” होती है।, “कुपर” का घनत्व $8.92 , \text{g/cm}^3$ होता है, कपर के परमाणु मान में बदलवान की गणना कीजिए।

स्वरूपण की सुरक्षा के लिए, हर वाक्य को एक ही पंक्ति में अनुवाद करेंगे।

एफसीसी जाल के मामले में, इकाई कक्ष के हर कक्ष में परमाणु की संख्या, z = 4 परमाणु होती है इसलिए, $$M=\frac{\mathrm{dN}_{\mathrm{A}} \mathrm{a}^{3}}{\mathrm{Z}}$$

$$=63.1 \mathrm{~ग्राम} / \mathrm{मोल}$$

तांत्रिक गुरுत्वाकर्षण का मान $=63.1 \mathrm{u}$

उदाहरण 1.5

चांदी सतह कक्ष का गठन करता है और इसके क्रिस्टल का एक्सरे स्टडी में प्रमंडल का कोन्डाइशन एज का व्याप कर लेता है। चांदी का घनत्व कीशोर (एटॉमिक मास = 107.9 u) की गणना करें।

क्योंकि जाल ccp है, इकाई कक्ष में चांदी के प्रमंडलों की संख्या = z = 4 चांदी का मोलर मास $=107.9 \mathrm{~ग्राम} \mathrm{~मोल}^{-1}=107.9 \times 10^{-3} \mathrm{~किलोग्राम} \mathrm{~मोल}^{-1}$

इकाई कक्ष की एजा लंबाई $=\mathrm{a}=408.6 \mathrm{~पीएम}=408.6 \times 10^{-12} \mathrm{~मीटर}$

घनत्व, $d=\frac{z \cdot \mathrm{M}}{\mathrm{a}^{3} \cdot \mathrm{N}_{\mathrm{A}}}$

$$ \begin{aligned} & =\frac{4 \times\left(107.9 \times 10^{-3} \mathrm{~ग्राम} \mathrm{~मोल}^{-1}\right)}{\left(408.6 \times 10^{-12} \mathrm{~मीटर}\right)^{3}\left(6.022 \times 10^{23} \mathrm{~मोल}^{-1}\right)}=10.5 \times 10^{3} \mathrm{~किलोग्राम} \mathrm{~मीटर}^{-3} \ & =10.5 \mathrm{~ग्राम} \mathrm{~सेमी}^{-3} \end{aligned} $$

इंटेक्स्ट प्रश्न

1.13 वर्गीकृत बंद खंड में एक मोलेक्यूल का द्विआयामी समन्बंधी संख्या क्या होता है?

1.14 एक मिश्रण षट्कोण बंद में गठन होता है। इसके 0.5 मोल के लिए कुल खाल की संख्या क्या होती है? इनमें से कितने तेत्राहेद्राल खाल होते हैं?

1.15 एक मिश्रण दो तत्वों एम और एन द्वारा गठित होता है। पदार्थ एन नेताराम बनाता है और एम के परमाणु तेत्राहेद्राल खालों का 1/3 भरते हैं। संयोजन का प्रतिरूप क्या है?

1.16 निम्नलिखित में से कौन से जालों में सबसे अधिक पैकिंग क्षमता है (i) साधारित घन (ii) शरीर-केंद्रित घन और (iii) षट्कोण बंद जाल?

1.17 एक तत्व जिसका मोलर मास 2.7×10-2 किलोग्राम मोल-1 है, एक घनत्वीय इकाई कक्ष बनाता है जिसकी परमानु संचार की लंबाई 405 pm है। यदि उसकी घनत्व 2.7×103 किलोग्राम मीटर-3 है, तो क्या घनत्वीय इकाई कक्ष की प्रकृति होगी?

1.9 ठोस में अव्यवस्थाएँ

हालांकि क्रिस्टलीय ठोस अपने घटक अणुओं के व्यवस्था में छोटी और लंबी सीमा के क्रम में आदेश होता है, फिर भी क्रिस्टल सही नहीं होते हैं। आमतौर पर एक ठोस बहुत सारे छोटे क्रिस्टलों का समूह होता है। इन छोटे क्रिस्टलों में दोष होते हैं। यह इसलिए होता है क्योंकि द्रव्यीकरण की प्रक्रिया तेज या मध्यम गति से होती है। जबकि जब संक्रिया की प्रक्रिया अत्यंत धीमी गति से होती है, तो एकल क्रिस्टल बनता है। इन क्रिस्टलों में भी दोष होते हैं। दोष संक्रियाओं की व्यवस्था में घटनाएं होती हैं। ये अनियमितताएँ पदार्थ के घटक अणुओं की व्यवस्था में अनियमितता या विचलन होती हैं। व्यापक अर्थ में, दोष संबंधित सदियों के परिसर में मान्य विचलन होते हैं। हम अपनी चर्चा को केवल दोष से ही सीमित करेंगे।

1.9.1 दोषों के प्रकार

पॉइंट दोषों को तीन प्रकार में वर्गीकृत किया जा सकता है: (i) स्टोइकियोमेट्रिक दोष (ii) अपशिष्ट दोष और (iii) गैर-स्टोइकियोमेट्रिक दोष।

(a) स्टोइकियोमेट्रिक दोष इस तरह के पॉइंट दोष हैं जो ठोस की स्टोइकियोमेट्री को बिगाड़ते नहीं हैं। इन्हें स्वाभाविक या थर्मोडायनेमिक दोष भी कहा जाता है। मूल रूप से ये दो प्रकार के होते हैं, रिक्ति दोष और अंतःस्थ दोष।

(i) रिक्ति दोष: जब कुछ घटित संधि स्थान खाली हो जाते हैं, तो क्रिस्टल को रिक्ति दोष (चित्र 1.27) होता है। इससे पदार्थ के घनत्व में कमी होती है। इस दोष का आकार भी जब किसी पदार्थ को गर्म किया जाता है तो विकसित हो सकता है।

(ii) अंतःस्थ दोष: जब कुछ पृष्ठांत तत्व (परमाणु या धातुलु) एक अंतर्वाही स्थान पर स्थानांतरित होते हैं, तो क्रिस्टल को अंतःस्थ दोष (चित्र 1.28) होता है। इस दोष से पदार्थ का घनत्व बढ़ता है।

रिक्ति और अंतःस्थ दोष जैसा कि पहले समझाया गया है, गैर-आयनिक ठोसों द्वारा दिखाया जा सकता है। आयनिक ठोसों को हमेशा विद्युतिम रूपरेखा बनाए रखना चाहिए। साधारण या अंतःस्थ दोषों के बजाय, वे इन दोषों को फ्रेंकेल और शॉट्की दोष के रूप में दिखाते हैं।

(iii) फ्रेंकेल दोष: यह दोष आयनिक ठोसों द्वारा दिखाया जाता है। छोटे आयन (आमतौर पर कैटाइन) को उसके सामान्य स्थान से एक अंतवही स्थान (चित्र 1.29) पर स्थानांतरित किया जाता है। इससे इसकी मूल स्थान पर रिक्ति दोष और नए स्थान पर अंतःस्थ दोष बनता है।

फ्रेंकेल दोष को भी तत्वीय दोष कहा जाता है। इससे ठोस के घनत्व में परिवर्तन नहीं होता है। फ्रेंकेल दोष विद्युतीय पदार्थों द्वारा दिखाया जाता है जिनमें आयनों के आकार में बड़ा अंतर होता है, उदाहरणार्थ, $\mathrm{ZnS, AgCl, AgBr}$ और $\mathrm{AgI}$ के कारण $\mathrm{Zn}^{2+}$ और $\mathrm{Ag}^{+}$आयनों के छोटे आकार।

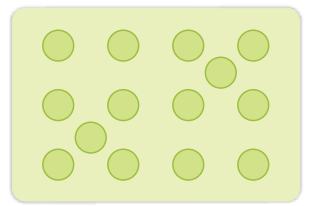
(iv) शॉट्की दोष: यह आयनिक ठोसों में बुनियादी रूप से रिक्ति दोष है। विद्युत समता बनाए रखने के लिए, गायब कैशन और एनियन की संख्या समान होती है (चित्र 1.30)।

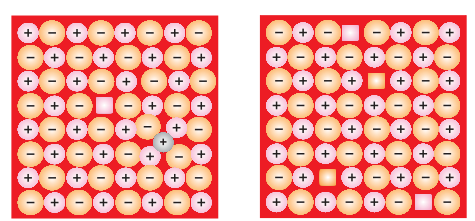
साधारण रिक्ति दोष की तरह, शॉट्की दोष भी पदार्थ का घनत्व कम करता है। आयनिक ठोसों में इन दोषों की संख्या बहुत महत्वपूर्ण होती है। उदाहरण के लिए, नैट्रियम क्लोराइड में कम से कम $10^{6}$ शॉट्की युग्म प्रति $\mathrm{cm}^{3}$ के लगभग होते हैं रूम तापमान पर। एक $\mathrm{cm}^{3}$ में लगभग $10^{22}$ आयन होते हैं। इस प्रकार, एक $10^{16}$ आयनों पर एक शॉट्की दोष होती है। शॉट्की दोष को ऐसे आयनिक पदार्थों द्वारा दिखाया जाता है जिनमें कैशन और एनियन लगभग समान आकार के होते हैं। जैसे, $\mathrm{NaCl, KCl, CsCl}$ और $\mathrm{AgBr}$। यह ध्यान देना चाहिए कि $\mathrm{AgBr}$ फ्रेंकेल और शॉट्की दोष दोनों दिखाता है।

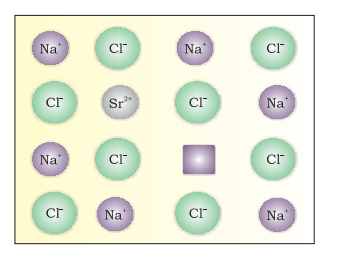
(b) अशुद्धता दोष: यदि थले $\mathrm{NaCl}$ में थोड़ी मात्रा में $\mathrm{SrCl_2}$ मिले हुए होता है, तो कुछ $\mathrm{Na}^{+}$ आयनों की स्थानें $\mathrm{Sr}^{2+}$ द्वारा भरी जाती हैं। प्रत्येक $\mathrm{Sr}^{2+}$ दो $\mathrm{Na}^{+}$ आयनों की जगह लेता है। इसमें एक आयन की स्थान पर कब्‍ज़ा किया जाता है और दूसरी स्थान खाली रहती है। ऐसे उत्पन्न होने वाले कैटानिक क्षूणक (cationic vacancies) की संख्या $\mathrm{Sr}^{2+}$ आयनों की संख्या के बराबर होती है। एक और इसी प्रकार का उदाहरण है $\mathrm{CdCl}_{2}$ और $\mathrm{AgCl}$ का ठोस विलयन।

(c) गैर-स्तोइकियोमेट्रिक दोष (Non-Stoichiometric Defects): अब तक विचार किए गए दोषों से ठोस विलयन की गणना को प्रभावित नहीं किया गया है। हालांकि, असंख्या गैर-स्तोइकियोमेट्रिक अविन्यासों वाले विद्युताकृष्ट ठोस जाने जाते हैं जिनमें उनके क्रिस्टल संरचनाओं के दोषों के कारण तत्वों का सामग्रीय अनुपात नहीं बनता है। ये दोष दो प्रकार के होते हैं: (i) धातुभार अविन्यास (metal excess defect) और (ii) धातुहीन अविन्यास (metal deficiency defect)।

(i) धातुभार अविन्यास : एक तत्वों के प्राप्तियों के लिए एक ऐनांदित खाने के कारण एकांत्रिक खाली स्थान ढीला देता है: नासियो एलाइड जैसे $\mathrm{NaCl}$ और $\mathrm{KCl}$ इस प्रकार के दोष को दर्शाते हैं। जब $\mathrm{NaCl}$ का क्रिस्टल सोडियम वाष्प के वातावरण में गर्म किया जाता है, तो सोडियम अणु स्वच्छता का सत्यापन के लिए क्रिस्टल की सतह पर निर्वाह होता है। $\mathrm{Cl}^{-}$ आयन में क्रिस्टल की सतह तक जाकर सोडियम अणु के साथ मिलकर $\mathrm{NaCl}$ मिलाते हैं। इसके परिणामस्वरूप पत्तन यात्रा से ही इलेक्ट्रॉन की नुकसान से सोडियम अणु मिलकर $\mathrm{Na}^{+}$ आयन बना देता है। निर्मित इलेक्ट्रान क्रिस्टल में विचरण करते हैं और एनाइटिक स्थानों को रोकते हैं (आदर्श १.३२)। इस परिणामस्वरूप क्रिस्टल में अब सोडियम की अधिकता होती है। एकांत्रिक स्थानों पर युनांधित इलेक्ट्रानों द्वारा भरे गए एनाइटिक स्थानों को एफ-केंद्र (जर्मन शब्द फ़ारबेंजेंटर से) कहते हैं। वे लाल रंग को $\mathrm{NaCl}$ के क्रिस्टलों में देते हैं। रंग इसलिए होता है क्योंकि जब वे पड़ती हुई प्रकाश की आवश्यक संश्लेषण से इन इलेक्ट्रानों के उत्सर्जन से उत्तेजित होते हैं। उस प्रतिदीप्ति से नासियो एलाइड द्वारा और विभिन्न रंग मिलाते हैं। उदाहरण के रूप में, लिथियम की अधिकता पिंक बनाती है और पोटेशियम की अधिकता की वजह से $\mathrm{KCl}$ के क्रिस्टलों को बैंगनी रंग या गुलाबी बना देती है।

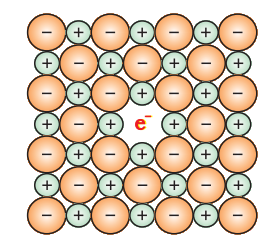
à ऐनाधिक अनुपाती गैर-स्तोइक दोष के कारण अतिरिक्त कैटियों की उपस्थिति के कारण धातुभार अविन्यास: तांबे का अधिकता धब्बें रंग का होता है। जब वह गर्म होने पर ऑक्सीजन खो देता है और पीला हो जाता है। $$ \mathrm{ZnO} \xrightarrow{\text { गर्म करना }} \mathrm{Zn}^{2+}+\frac{1}{2} \mathrm{O_2}+2 \mathrm{e}^{-} $$

अब क्रिस्टल में तांबे की अतिरिक्तता होती है और इसका सूत्र बन जाता है $\mathrm{Zn_1+\mathrm{x}} \mathrm{O}$। अतिरिक्त $\mathrm{Zn}^{2+}$ आयन अंतरिख्या स्थानों पर चले जाते हैं और इलेक्ट्रॉन्स पड़ोसी अंतरिख्या स्थानों पर।

(ii) धातुहीन अविन्यास (Metal Deficiency Defect)

कई ठोस वस्तुएं होती हैं जो सं॰ योजक संरचना में तैयार करना कठिन होता है और योजक प्रमाण की तुलना में मेटल की कम मात्रा प्रमाण में पाई जाती है। इस प्रकार का एक साधारण उदाहरण $\mathrm{FeO}$ है जो अधिकांश ओरवेमुक्ति $\mathrm{Fe}\circ प्रमाण$ के साथ पाई जाती है। यह वास्तविक रेंज $\mathrm{Fe}\circ.९३$ से $\mathrm{Fe}_\circ.९६$ तक हो सकती है। $\mathrm{FeO}$ के क्रिस्टलों में कुछ $\mathrm{Fe}^{2+}$ कैटाइयों की कमी होती है और उत्पोषित धन की हानि $\mathrm{Fe}^{3+}$ आयनों की उपस्थिति से पूरी होती है।

1.10 विद्युतीय गुण

ठोस पदार्थों में विद्युतीय निर्देश सहजता की आश्चर्यजनक विविधता प्रदर्शित करते हैं, जो $10^{-20}$ से $10^7$ ओह्म मीटर की रेंज तय करती है। ठोस पदार्थों को उनकी निर्देश सहजता के आधार पर तीन वर्गों में वर्गीकृत किया जा सकता है।

(i) प्रवाहक: $10^4$ से $10^7$ ओह्म मीटर की रेंज में निर्देश सहजता वाले ठोस कोन्डक्टर कहलाते हैं। धातुओं में $10^7$ ओह्म मीटर की रेंज में निर्देश सहजता होती है जो अच्छे कोन्डक्टर होते हैं।

(ii) इंसुलेटर्स: ये वे ठोस होते हैं जिनकी निर्देश सहजता बहुत कम होती है, $10^{-20}$ से $10^{-10}$ ओह्म मीटर की रेंज में।

(iii) सेमीकंडक्टर्स: ये वे ठोस होते हैं जिनकी निर्देश सहजता $10^{-6}$ से $10^4$ ओह्म मीटर की रेंज में होती है।

1.10.1 धातुओं में विद्युत की निर्देश सहजता

एक प्रवाहक इलेक्ट्रॉन या आयन के गतिमान के माध्यम से विद्युत सहजता कर सकता है। धातुओं की निर्देश सहजता पर संचारित विद्युत क्षेत्र और इलेक्ट्रोलाइट्स पर भी होती है।

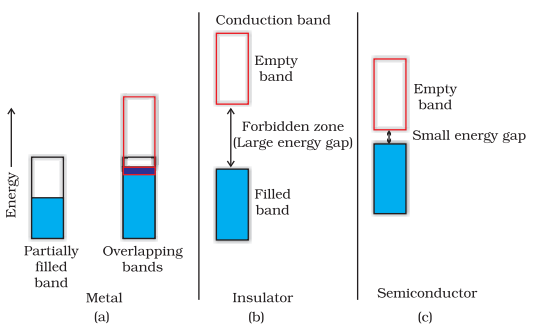
धातुओं की निर्देश सहजता स्थिर और घोलित अवस्था दोनों में होती है। धातुओं की निर्देश सहजता एक परम प्रतीति प्रति अणु उपलब्ध योजक इलेक्ट्रोनों की संख्या पर निर्भर करती है। धातु अणुओं के परमभूत आकाशीय वेतावरण अणुओं का एक मैन्युलर आकाशीय वेतावरण बनाता है जो एक ताल के रूप में निकटतम होते हैं। यदि यह ताल आंशिक रूप से भरी होता है या इसकी श्रेणी के उच्चतर बंद निर्धारित केंद्रन ताल के साथ ओवरलैप होता है, तो इलेक्ट्रॉनों के तनावित विद्युत श्रवण और धातु सारणी प्रदर्शित करने के लिए आसानी से छेद कर सकते हैं। (चित्र 1.33 ए)

यदि परंपरागत पूरी हुई परिवर्तनीय स्रोत की जटिलता और अगले उच्चतम अनकथीकरणीय ताल (निर्देश सहजता) के बीच इन्तरबैंड को विद्युतຯ धातुओं की प्रत्यय हो सकती है और ऐसी कोइस्लमार निर्देश सहजता (Figure 1.33 b)।

1.10.2 सेमीकंडक्टर्स में विद्युत सहजता

सेमीकंडक्टर्स के मामले में पाठक ताल का अंतरमांध्र, महवेता ताल और गनत्र ताल का अंतर कम होता है (चित्र 1.33 c)। इसलिए, कुछ इलेक्ट्रॉन जो महवेता ताल में छलांग ले सकते हैं और कुछ निर्देश सहजता प्रदर्शित कर सकते हैं। सेमीकंडक्टर्स की विद्युतीय सहजता तापमान में बढ़ने से बढ़ती है, क्योंकि इलेक्ट्रॉनों की अधिक संख्या महवेता ताल में छलांग ले सकती है। सिलिकॉन और जर्मेनियम नामक पदार्थ इस प्रकार का व्यवहार दिखाते हैं और संयोजी सेमीकंडक्टर्स कहलाते हैं।

इन प्राकृतिक स्वामी संगठनों की

जर्मेनियम और सिलिकॉन समूह 14 के तत्व हैं और इसलिए, चार का एक विशेष वालेंस हैं और डायमंड में की तरह चार बांधते हैं। समूह 13 और 15 या 12 और 16 की मिश्रण बनाकर बड़ी संख्‍या में ठोस अवस्था के तत्व तैयार किए गए हैं जो कि Ge या Si में चार की औसत रासायनिकता का नकल करते हैं। समूह $13-15$ के प्रमुख यौज्य हैं InSb, AlP और GaAs। गैलियम ऑर्सेनाइड (GaAs) सेमीकंडक्‍टर्स की बहुत तेज प्रतिक्रिया होती है और सेमीकंडक्‍टर उपकरणों के डिज़ाइन में क्रांतिकारी बदलाव लाया है। ZnS, CdS, CdSe और HgTe groups $12-16$ के संयोजन के उदाहरण हैं। इन यौजों में, बांध सही तरह से कोवैलेंट नहीं होती है और आयनी गुणता दो तत्वों की इलेक्ट्रोनिगेटिविटी पर निर्भर करती है।

इसके रूपांतरण धातु धातु ऑक्साइड में विद्युतीय गुणों में विभेद दिखाते हैं। TiO, $\mathrm{CrO_2}$ और $\mathrm{ReO_3}$ धातु जैसे मेटलों की तरह व्यवहार करते हैं। रेनियम आक्साइड, $\mathrm{ReO_3}$ अपनी चोंदीता और दिखावट में धातुज कॉपर की तरह होता है। विशेष अन्य ऑक्साइड जैसे VO, $\mathrm{VO_2}, \mathrm{VO_3}$ और $\mathrm{TiO_3}$ तापमान के आधार पर धातुज या विद्युतीय गुणों को दिखाते हैं।

1.11 चुम्बकीय गुण

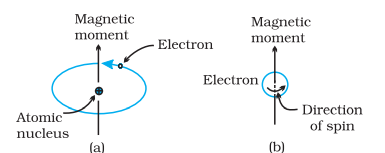
प्रत्येक पदार्थ के कुछ चुम्बकीय गुण जुड़े होते हैं। इन गुणों की मूल उत्पत्ति इलेक्ट्रॉनों में होती है। प्रत्येक इलेक्ट्रॉन परमाणु में एक छोटी सी चुम्बक की तरह व्यवहार करता है। इसका चुम्बकीय लम्बन दो तरह की गतियों (i) परिभाषिते गति (ii) इलेक्ट्रॉन के अपने अक्ष पर घूमने की (चित्र १.३५) से होता है। एलेक्ट्रॉन एक चार्जयुक्त कण होता है और इन गतियों को प्राप्त करता है, जिससे यह एक छोटा धारित्रीक परिधि मानित होता है। इस प्रकार, प्रत्येक इलेक्ट्रॉन के साथ स्थायी चिकनी और आवरती धारित्रीकयुक्त होती है। इस चुम्बकीय लम्बन का आनंदंग्रंथ बहुत ही छोटा और यह यूनिट जिसे बोह्र मैग्नीटोन मानते हैं, वह μB के नाम से होता है। यह 9.27 × 10–24A m2 के बराबर होता है।

अपने चुम्बकीय गुणों के आधार पर, पदार्थों को पांच श्रेणियों में वर्गीकृत किया जा सकता है: (i) पैराचुंबकीय (ii) विराचुंबकीय (iii) परधातुचुंबकीय (iv) एंटी-परधातुचुंबकीय और (v) चेकरदार-परधातुचुंबकीय।

(i) पैराचुंबकिता: पैराचुंबकित पदार्थ किसी चुंबकीय क्षेत्र द्वारा कम आकर्षित होते हैं। वे एक चुंबकीय क्षेत्र में, उसी दिशा में चुंबकित होते हैं। वे चुंबकीय क्षेत्र के अभाव में अपनी चुंबकिता खो देते हैं। पैराचुंबकिता एक या उससे अधिक अस्थायी इलेक्ट्रॉनों की उपस्थिति के कारण होती है जो चुंबकीय क्षेत्र द्वारा आकर्षित होते हैं। $\mathrm{O_2}, \mathrm{Cu}^{2+}, \mathrm{Fe}^{3+}, \mathrm{Cr}^{3+}$ कुछ ऐसे पदार्थों के उदाहरण हैं।

(ii) विराचुंबकिता: विराचुंबकिता एक ही दिशा में चुंबकीय क्षेत्र द्वारा कम द्वारा कम आकर्षित होते हैं। $\mathrm{H_2} \mathrm{O}, \mathrm{NaCl}$ और $\mathrm{C_6} \mathrm{H_6}$ कुछ ऐसे पदार्थों के उदाहरण हैं। वे एक चुंबकीय क्षेत्र में, उसी विपरीत दिशा में चुंबकीय होते हैं। विराचुंबित पदार्थों में सभी इलेक्ट्रॉन पीरित होते हैं और कोई उपलब्ध इलेक्ट्रॉन नहीं होते हैं। इलेक्ट्रॉनों के पीरित होने दृष्टिकोण से चुंबकीय-लम्बिता की खो देते हैं।

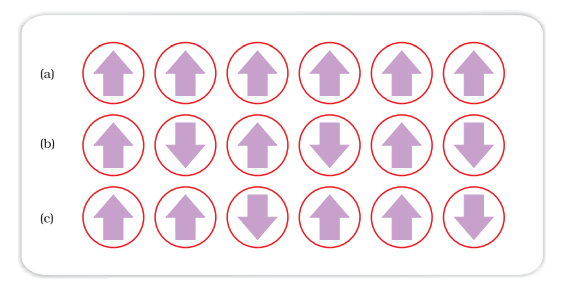
(iii) धातुवधिरोहीता: लोहा, कोबाल्ट, निकेल, गैडोलिनियम और क्रो2 जैसी कुछ पदार्थ धातुतापरवर्तनीय पदार्थ द्वारा बहुत मजबूती से आकर्षित किए जाते हैं। ऐसे पदार्थों को धातुवधी पदार्थ कहा जाता है। मजबूत आकर्षण के अलावा, इन पदार्थों को स्थायी रूप से चुंबककृत किया जा सकता है। ठोस अवस्था में, धातुवधी पदार्थों के धातु आयोनों को छोटे क्षेत्रों में समूहीकृत किया जाता है, जिन्हें डोमेन कहा जाता है। इस प्रकार, प्रत्येक डोमेन छोटा चुंबक के रूप में कार्य करता है। एक धातुवधी पदार्थ के अचुंबित टुकड़े में डोमेन यादृच्छिक रूप से असंयुक्त होते हैं और उनके चुंबकीय क्षण रद्द हो जाते हैं। जब पदार्थ एक चुंबकीय फ़ील्ड में रखा जाता है तो सभी डोमेन चुंबकीय फ़ील्ड की दिशा में संचारित हो जाते हैं (चित्र 1.36 a) और एक मजबूत चुंबकीय प्रभाव पैदा होता है। चुंबकीय फ़ील्ड को हटाया जाने पर भी यह डोमेनों का समूहीकरण बरकरार रहता है और धातुवधी पदार्थ एक स्थायी चुंबक बन जाता है।

(iv) विरोधी धातुतापर्वचकता: जैसे MnO विरोधी धातुतापर्वचकता दिखाने वाले पदार्थों को फाराईसँक्त्री पदार्थ के डोमेन संरचना होती है, लेकिन उनके डोमेन विपरीत दिशाओं में होते हैं और एक दूसरे के चुंबकीय क्षण को रद्द करते हैं (चित्र 1.36 b)।

(v) धातुसंपेदभूती: धातुसंपेदभूती देखी जाती है जब पदार्थ के डोमेनों के चुंबकीय क्षण बराबर संख्या में परालेल और विपरीत दिशाओं में सजीव प्रकार में बराबर होते हैं (चित्र $1.32 \mathrm{c}$)। ये पदार्थ धातुवधी पदार्थों की तुलना में मजबूत चुंबकीय क्षेत्र द्वारा कम दर्जे से चुंबकीय फ़ील्ड द्वारा आकर्षित होते हैं। $\mathrm{Fe}{3} \mathrm{O}{4}$ (म्याग्नेटाइट) और $\mathrm{MgFe}{2} \mathrm{O}{4}$ और $\mathrm{ZnFe}{2} \mathrm{O}{4}$ जैसे फेर्राइट इस प्रकार के पदार्थों की उदाहरण हैं। यह पदार्थ गर्म करने पर भी धातुसंपेदभूती खो देते हैं और पैराचुंबकीय हो जाते हैं।

अंत:अलेख प्रश्न

1.18 ऊष्मीय रूप से एक ठोस पदार्थ को किस प्रकार की दोष उत्पन्न हो सकती है? उससे कौन सी भौतिक गुण प्रभावित होती है और उसके कैसे प्रभावित होती है?

1.19 किस प्रकारीय रूप से द्योतिपूर्ण दोष को दर्शाती है: (i) जिंग्क सल्फाइड (ii) चांदी ब्रोमाइड

1.20 जब उसमें आयामांत लोहे द्वारा अविशुद्धिकरण किया जाता है तो आयामान्त्रात्मक ठोस में रिक्तियां कैसे प्रवेश करती हैं?

1.21 धातु अतिशेष दोष के कारण आनियक संपेदभूत धातु पर रंग विकसित होता है। उपयुक्त उदाहरण की सहायता से समझाएं।

1.22 एक सूत्र्य तत्व को आयामांत्रात्मक द्वारा n-प्रकार सेमीकंडक्टर में बदल दिया जाना है। इसके लिए यह आयामान्त्री को इस समूह से होना चाहिए?

1.23 स्थायी चुंबक, धातुवधी या धातुसंपेदभूती, कौन से प्रकार के पदार्थ बेहतर स्थायी चुंबक बनाएंगे? अपने उत्तर का समर्थन कीजिए।

संक्षेपण

सॉलिड्स की निश्चित मास, आयतन और आकृति होती है। इसका कारण है कि उनके घटक कणों की स्थिति में तय रेखा, छोटी दूरियां और उनके बीच मजबूत संवेदनशीलता होती है। अस्थिर सॉलिड में, घटक कणों की व्युत्क्रमण सीमा केवल छोटी होती है और फलस्वरूप वे सुपर कूल्ड सामग्री की तरह व्यवहार करते हैं, वे तापन बिंदुओं के स्पष्ट योगान्यता नहीं रखते हैं और सर्वत्रिकता प्राप्त करते हैं। क्रिस्टलाइन सॉलिड में, उनके घटक कणों के व्युत्क्रमण में दीर्घ संवेदनशीलता होती है। उनके पास स्पष्ट तापन बिंदु होते हैं, वे दिशानुभूत होते हैं और उनके कण परिचय आकार होते हैं। क्रिस्टलाइन सॉलिड्स की गुणधर्म उनके घटक कणों के बीच के संवेदनशीलता के स्वभाव पर निर्भर करती हैं। इस आधार पर, उन्हें चार श्रेणियों में विभाजित किया जा सकता है, जैसे: आणवीय, इयनिक, धातुरसायनिक और सहसंबद्ध सॉलिड्स। इनकी गुणधर्म विशिष्टता में व्याप्त अंतर होता है।

क्रिस्टलाइन सॉलिड्स में घटक कणों को एक नियमित पैटर्न में व्यवस्थित किया जाता है जो क्रिस्टल के भीतर फैलता है। यह व्यवस्था आमतौर पर तीन आयामी बिंदु सरणी के रूप में चित्रित की जाती है जो क्रिस्टल लैटिस कहलाती है। प्रत्येक लैटिस पॉइंट अंतरिक्ष में एक कण की स्थान देता है। संपूर्ण, चौदह प्रकार की लैटिस मुमकिन हैं जिन्हें ब्राविस लैटिस कहा जाता है। प्रत्येक लैटिस अपने छोटे विशेष भाग यानी यूनिट सेल को दोहराने द्वारा प्राप्त किया जा सकता है। एक यूनिट सेल अपनी किनारों की लंबाईयों और इन किनारों के बीच तीन कोणों के बीच की त्रिकोणीय रेखाओं के द्वारा विशिष्टता से चरित्रित होता है। यूनिट सेल या मूल सेल या तो मूलभूत हो सकती है जिसमें केवल किनारे की पोजीशन पर कण होते हैं या केंद्रित हो सकती है। केंद्रित यूनिट सेलों में अतिरिक्त कण उनके शरीर केंद्र (शरीर केंद्रित), हर ओर के केंद्र पर (मुख्य-केंद्रित) या दो विपरीत ओरों के केंद्र पर होते हैं (अंत-केंद्रित)। प्राय: सात प्रकार की मूलांकीत यूनिट सेलें होती हैं। केंद्रित यूनिट सेलों को भी मिला कर, संपूर्ण में चौदह प्रकार की यूनिट सेलें होती हैं, जो संपूर्ण ब्राविस लैटिस के नतीजे होती हैं।

कणों के क्लोज-पैकिंग के परिणामस्वरूप दो अत्यधिक कुशल लैटिसेस होते हैं, हेक्सेगोनल क्लोज-पैक्ड (एचसीपी) और क्यूबिक क्लोज-पैक्ड (सीसीपी)। इनमें से आपस में 74% अंतरिक्ष भरा होता है। शेष अंतरिक्ष दो प्रकार के खालियों-ऑकटाहेड्रल खालीयों और चतुर्भुजीय खालीयों के रूप में मौजूद होता है। अन्य प्रकार का पैकिंग क्लोज-पैकिंग नहीं होता है और कणों का कम कुशल पैकिंग होता है। जबकि बॉडी-केंद्रित क्यूबिक लैटिस (बीसीसी) में 68% अंतरिक्ष भरा होता है, सरल घनवृत्तीय लैटिस में केवल 52.4% अंतरिक्ष भरा होता है।

सामग्री: ठोस रचना में पूर्णता नहीं होती है। उनमें विभिन्न प्रकार की अपूर्णताओं या दोष होते हैं। बिंदुदोष और रेखा दोष सामान्य तरह के दोष होते हैं। बिंदुदोष के तीन प्रकार होते हैं - स्तोइचियोमैटिक दोष, पदार्थद्रव दोष और अस्तोइचियोमैटिक दोष। खाली स्थान दोष और इंटरस्टिशियल दोष स्तोइचियोमैटिक बिंदुदोष के दो मूल प्रकार होते हैं। आयनिक ठोसों में, ये दोष Frenkel और Schottky के रूप में मौजूद होते हैं। पदार्थद्रव दोष द्रव्य में एक द्रव्यमिलन मौजूद होने के कारण होते हैं। आयनिक ठोसों में, जब आयनिक पदार्थ मुख्य मिश्रण की तुलना में अलग मूल्यांकन रखता है, तो कुछ खाली स्थान बनते हैं। गैरस्थोइचियोमैटिक दोष में धातु के अतिरिक्त प्रकार और धातु की कमी के प्रकार होते हैं। कभी-कभी ऑयलिक ऊपर होने वाली मात्रा के द्वारा जाँचे जाने वाले दोष धांतिमल में परिभाषित किए जाते हैं जो इलेक्ट्रॉनिक गुणों या संरचनाओं के साथ जुड़े हैं। ठोसों में पैरामैगनेटिज़म, डायमैगनेटिज़म, फेरोमैगनेटिज़म, एंटीफेरोमैगनेटिज़म और फेर्रिमैगनेटिज़म जैसे कई प्रकार की चुंबकीय गुणधर्म दिखाते हैं। ये गुणधर्म ऑडियो, वीडियो और अन्य रिकॉर्डिंग उपकरणों में उपयोग होते हैं। इन सभी गुणधर्मों को उनके इलेक्ट्रॉनिक संरचना या संरचनाओं के साथ सम्बद्ध किया जा सकता है।

अभ्यास

1.1 ‘अमोर्फस’ शब्द का परिभाषा दें। अमोर्फस ठोसों के कुछ उदाहरण दें।

1.2 शीशा को क्वार्ट्ज के समान एक ठोस से किस बात से अलग बनाता है? क्वार्ट्ज को कितनी शर्तों के तहत शीशे में बदला जा सकता है?

1.3 निम्नलिखित ठोसों को आयनिक, धातु, आणविक, नेटवर्क (संयुक्त वास्तु) या अमोर्फस में वर्गीकृत करें।

(i) टेट्रा फास्फोरस डिऑक्साइड $\left(\mathrm{P_4} \mathrm{O_10}\right) \quad$ (vii) ग्राफाइट

(ii) एमोनियम फॉस्फेट $\left(\mathrm{NH_4}\right)_{3} \mathrm{PO_4} \quad$ (viii) पीतल

(iii) $\mathrm{SiC}$

(ix) $\mathrm{Rb}$

(iv) $\mathrm{I_2}$

(v) $\mathrm{P_4}$

(x) $\mathrm{LiBr}$

(vi) प्लास्टिक

(xi) $\mathrm{Si}$

1.4 (i) ‘समन्वयांक संख्या’ शब्द का क्या अर्थ होता है?

(ii) धातु अण्डाकार संरचना में परमाणु अणुओं की समन्वयांक संख्या क्या होती है?

(a) एक घनत्व निकट-रखा संरचना में?

(b) एक शरीर केंद्रित घनत्व संरचना में?

1.5 यदि आप एक अज्ञात धातु का आणुमास्य जानते हैं, तो उसके घनत्व और इकाई सेल के आयाम को जानकर आप कैसे तय कर सकते हैं? समझाएं।

1.6 ‘क्रिस्टल की स्थिरता उसके पिघलने के अंदाजे से प्रतिबिंबित होती है।’ टिप्पणी करें। डेटा किताब से ठोस पानी, इथाइल एल्कोहल, डाइइथाइल इथर और मिथेन के पिगलने बिन्दुओं का मेल तथा घनत्व का संग्रह करें। इन मोलेकुलों के बीच इंटरमोलेक्युलर बालों के बारे में आप क्या कह सकते हैं?

1.7 निम्नलिखित शब्दों के बीच आप कैसे भेद करेंगे:

(i) षष्ठकोणीय घनत्व-रचना और घनत्व-रचना-इकाई पक्षीय घनत्व?

(ii) क्रिस्टल ग्रिड और इकाई कोशिका?

(iii) त्रिताशी रिक्त स्थान और अष्टाभूजीय रिक्त स्थान?

1.8 निम्नलिखित ग्रिड की एक इकाई कोशिका में कितनी लैटिस बिंदुएं होती हैं?

(i) मुख्य-अणु वर्तमान घनत्व केंद्रित

(ii) मुख्य-अण्डाकार चतुर्वकरित

(iii) शरीर-केंद्रित

1.9 व्याख्या करें

(i) धातुय और आयनिक क्रिस्टल के बीच समानताएं और अंतर।

(ii) आयनिक ठोसों कठोर और भंगुर होते हैं।

1.10 एक मेटल क्रिस्टल की पैकिंग की कुशलता कीगणना करें (असुमिश्रित क्रिस्टल के मामले में)

  (i) सरल घनसरक
  (ii) शरीर-केंद्रित घनसरक
  (iii) द्विमुखीय सरह-केंद्रित घनसरक (यहाँ मान स्पर्शित होने वाले परमाणुओं का है )

1.11 चांदी fcc रेखागणित में तैनात होती है। यदि सेल की किनारे की लंबाई $4.07 \times 10^{-8}$ $\mathrm{cm}$ है और घनत्व $10.5 \mathrm{~g} \mathrm{~cm}^{-3}$ है, तो चांदी का परमाणुजीवी भार की गणना करें।

1.12 एक घनवर्गीय स्थिर दो तत्वों $ \mathrm{P}$ और $ \mathrm{Q}$ से बना होता है। क्या यह यौगिक की सूत्र है? $\mathrm{P}$ और $ \mathrm{Q}$ की समन्वय संख्याएं क्या हैं?

1.13 नाइबियम शरीर-केंद्रित घनसरंचना में तैनात होता है। यदि घनत्व $8.55 \mathrm{~g} \mathrm{cm}^{-3}$ है, तो नाइबियम के परमाणुजीवी तत्व की तत्वीय त्रिज्या की गणना करें, जिसमें उसका परमाणुजीवी भार $93 \mathrm{u}$ है।

1.14 यदि ऑक्टहीड्रल शून्यस्थान का त्रिज्या $\mathrm{r}$ है और क्लोजपैकिंग में स्थित परमाणुओं का त्रिज्या $R$ है, तो $\mathrm{r}$ और $R$ के बीच संबंध निर्धारित करें।

1.15 तांबे को फेस-केंद्रित घनसरक में रेखागणित किया जाता है, जिसकी किनारे की लंबाई $3.61 \times 10^{-8} \mathrm{~cm}$ है। इसका घनत्व $8.92 \mathrm{~g} \mathrm{~cm}^{-3}$ के साथ माप बनता है। दिखाएं कि गणनित घनत्व इसके मापित मान के साथ सहमत है।

1.16 विश्लेषण से पता चलता है कि निकेल ऑक्साइड का सूत्र $ \mathrm{Ni_0.98} \mathrm{O_1.00}$ होता है। निकेल का कितना भाग $ \mathrm{Ni}^{2+}$ और $ \mathrm{Ni}^{3+}$ आयनों के रूप में मौजूद है?

1.17 एक सेमीकंडक्टर क्या है? सेमीकंडक्टर के दो प्रमुख प्रकारों की विवरण करें और उनकी चलन पद्धति का तुलनात्मक विवेचन करें।

1.18 गैरस्थायी स्थिरीकृत कपरूस ऑक्साइड, $ \mathrm{Cu_2} \mathrm{O}$, प्रयोगशाला में बनाया जा सकता है। इस ऑक्साइड में, कॉपर से ऑक्सीजन अनुपात थोड़ा सा $2: 1$ से कम होता है। क्या आप इस तथ्य का हिसाब लगा सकते हैं कि यह पदार्थ p-प्रकार का सेमीकंडक्टर होता है?

1.19 फेरिक ऑक्साइड को शहपटी घनसरणीय आरेख में संरचित किया जाता है, जहां हर तीनों ऑक्टेहीड्राल खाली स्थानों में फेरिक आयन तैनात होते हैं। फेरिक ऑक्साइड का सूत्र निर्धारित करें।

1.20 निम्नलिखित में से प्रत्येक को p-प्रकार या n-प्रकार का सेमीकंडक्टर मान्यांकन करें: (i) In द्वारा प्रदीप्त जर्मेनियम (Ge) (ii) B द्वारा प्रदीप्त सिलिकॉन (Si)