SATHEE: wave-optics Question 43

wave-optics Question 43

Question: Q. 7. Two polaroids, $P_{1}$ and $P_{2}$ are ‘set-up’ so that their ‘pass-axes’ are ‘crossed’ with respect to each other. A third polaroid, $P_{3}$ , is now introduced between these two so that its ‘pass-axis’ makes an angle $θ$ with ‘pass-axis’ of $P_{1}$ .

A beam of unpolarised light, of intensity $I$ , is incident on $P_{1}$ . If the intensity of light, that gets transmitted through this combination of three polaroids, is $I^{'}$ , find the ratio $(\frac{I^{'}}{I})$ when $θ$ equals :

(i) $30^{\circ}$ , (ii) $45^{\circ}$ .

A[Delhi Comptt., 2016]

Intensity of unpolarised light is given as $I$ , It becomes $\frac{I}{2}$ on passing through polaroid $P_{1}$

$∴$ Using law of Malus, for the intensity passing through $P_{3}$

$I_{1} = (\frac{I}{2}) \cos^{2} θ$

This intensity $I_{1}$ is incident on $P_{2}$

Hence using law of Malus for Polaroid $P_{2}$

$I^{'} = I_{1} \cos^{2} (90^{\circ} - θ)$

$= \frac{I}{2} \cos^{2} θ [\cos^{2} (90^{\circ} - θ)]$

$= \frac{I}{8} (2 \cos θ \sin θ)^{2}$

$1 / 2$

$= \frac{I}{8} (\sin 2 θ)^{2}$

$1 / 2$

(i) When

$θ = 30^{\circ}$

Then

$I^{'} = \frac{I}{8} {(\sin 60^{\circ})}^{2}$

$\Rightarrow \frac{I^{'}}{I} = \frac{3}{32}$

(ii) When $θ = 45^{\circ}$

$\Rightarrow \frac{I^{'}}{I} = \frac{1}{8}$

[CBSE Marking Scheme 2016]

Commonly Made Error

Many students used a final long and tedius method to obtain final Intensity.

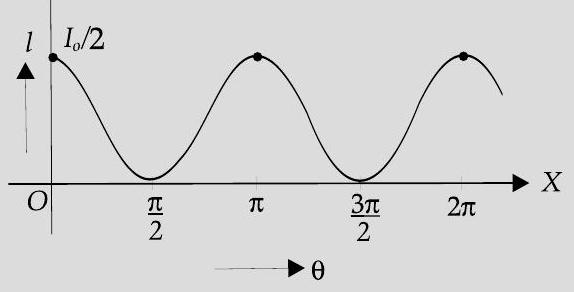
Q. 8. (a) When an unpolarized light of intensity $I_{0}$ is passed through a polaroid, what is the intensity of the linearly polarized light? Does it depend on the orientation of the polaroid? Explain your answer.

(b) A plane polarized beam of light is passed through a polaroid. Show graphically the variation of the intensity of the transmitted light with angle of rotation of the polaroid in complete one rotation.

[CBSE Comptt. 2018]

Show Answer

Solution:

Ans. (a) Intensity of linearly polarized light $1 / 2$ Dependence on orientation Explanation

(b) Graphical representation

(a) The intensity of the linearly polarized light would $\frac{I_{0}}{2}$ .

$1 / 2$

No; it does not depend on the orientation. $1 / 2$

Explanation : The polaroid will let the component of the unpolarized light, parallel to its pass axis, to pass through it irrespective of its orientation.

(b) We have

$I = I_{0} \cos^{2} θ$

$∴$ The graph is as shown below

[CBSE Marking Scheme 2018]

Long Answer Type Questions

(5 marks each)

Wave Optics

wave-optics Question 43

Commonly Made Error

Long Answer Type Questions

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Wave Optics

wave-optics Question 43

Commonly Made Error

Long Answer Type Questions

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu