Question: Q. 7. Two polaroids,
A beam of unpolarised light, of intensity
(i)
A[Delhi Comptt., 2016]
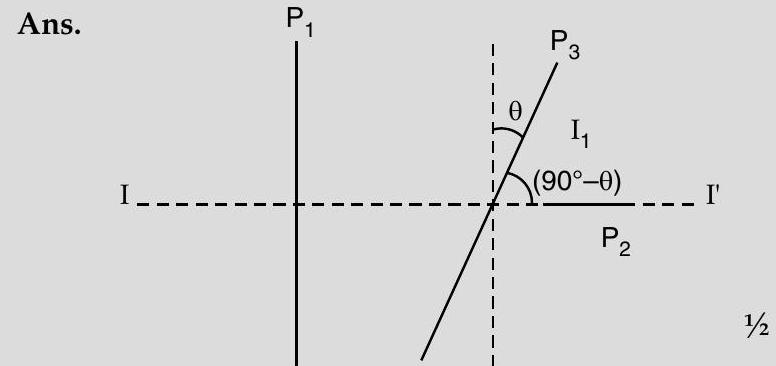
Intensity of unpolarised light is given as
This intensity
Hence using law of Malus for Polaroid
(i) When
Then
(ii) When
[CBSE Marking Scheme 2016]
Commonly Made Error
- Many students used a final long and tedius method to obtain final Intensity.
Q. 8. (a) When an unpolarized light of intensity
(b) A plane polarized beam of light is passed through a polaroid. Show graphically the variation of the intensity of the transmitted light with angle of rotation of the polaroid in complete one rotation.
[CBSE Comptt. 2018]
Show Answer
Solution:
Ans. (a) Intensity of linearly polarized light
(b) Graphical representation
(a) The intensity of the linearly polarized light would
No; it does not depend on the orientation.
Explanation : The polaroid will let the component of the unpolarized light, parallel to its pass axis, to pass through it irrespective of its orientation.
(b) We have
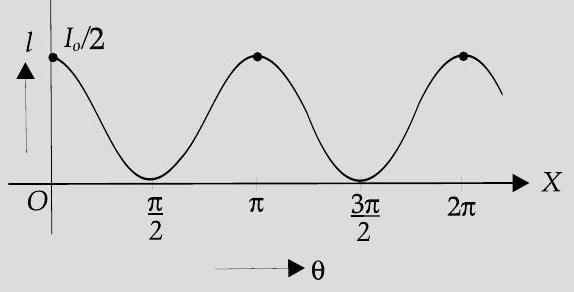
[CBSE Marking Scheme 2018]
Long Answer Type Questions
(5 marks each)






