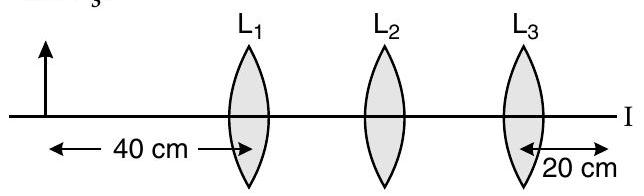
SATHEE: ray-optics-and-optical-instruments Question 37

ray-optics-and-optical-instruments Question 37

Question: Q. 6. You are given three lenses $L_{1}, L_{2}$ and $L_{3}$ each of focal length $20 cm$ . An object is kept at $40 cm$ in front of $L_{1}$ . The final real image is formed at the focus $I$ of $L_{3}$ . Find the separations between $L_{1^{'}} L_{2}$ and $L_{3}$ .

[O.D. I, II, III 2012]

$\begin{aligned} f_{3} & = + 20 cm, v_{3} = 20 cm \frac{1}{20} & = \frac{1}{20} + \frac{1}{u_{3}} \end{aligned}$

$\Rightarrow u_{3} = \infty$

$1 / 2$

It shows that $L_{2}$ must render the rays parallel to the common axis. It means that the image $(I_{1})$ , formed by $L_{1}$ , must be at a distance of $20 cm$ from $L_{2}$ (at the focus of $L_{2}$ )

Therefore, distance between $L_{1}$ and $L_{2} (= 40 + 20)$ $= 60 cm$ and distance between $L_{2}$ and $L_{3}$ can have any value.

[CBSE Marking Scheme 2012] 1/22

Detailed Answer :

Given,

$f_{1} = f_{2} = f_{3} = 20 cm$

For lens, $L_{1}$

$\begin{aligned} u & = - 40 cm f & = 20 cm \frac{1}{v} - \frac{1}{u} & = \frac{1}{f} \frac{1}{v} & = \frac{1}{u} + \frac{1}{f} \frac{1}{v} & = - \frac{1}{40} + \frac{1}{20} \frac{1}{v} & = \frac{1}{40} v & = 40 cm \end{aligned}$

( + ve sign shows it is right hand side of lens $L_{1}$ )

Now for $L_{3}$ , the final image is at its focus, that means $v_{3} = + 20 cm$ . Hence $u_{3} = \infty$

Now, since image of the object $A B$ formed by convex lens $L_{2}$ is virtual object for $L_{3}$ , therefore $v_{2} = \infty$ .

Hence for lens $L_{2}, u_{2} = ?, f_{2} = 20 cm$ and $v_{2} = \infty$ . Using the lens formula,

$\begin{aligned} \frac{1}{v_{2}} - \frac{1}{u_{2}} & = \frac{1}{f_{2}} \Rightarrow \frac{1}{\infty} - \frac{1}{u_{2}} & = \frac{1}{20} u_{2} & = - 20 cm \end{aligned}$

So, the separation between $L$ and $L_{2}$

$= 40 + 20 = 60 cm$

As $v_{2} = \infty$ and $u_{3} = \infty$ , therefore the distance between $L_{2}$ and $L_{3}$ does not matter it may take any value because image by $L_{2}$ is formed at infinity.

(AI Q. 7. A convex lens of focal length $20 cm$ is placed coaxially with a convex mirror of radius of curvature $20 cm$ . The two are kept at $15 cm$ from each other. A point object lies $60 cm$ in front of the convex lens. Draw a ray diagram to show the formation of the image by the combination. Determine the nature and position of the image formed. [O.D. I, II, III 2014]

Show Answer

Solution:

Ans.

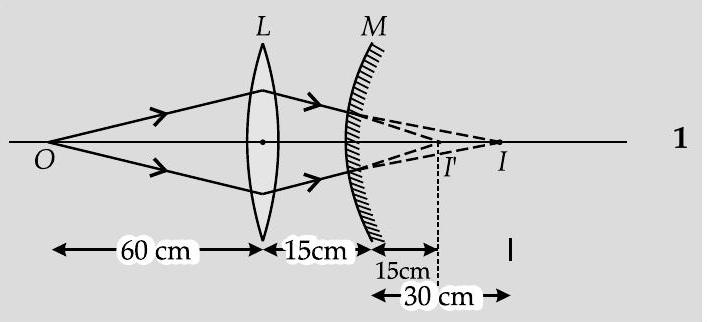
For the convex lens, $u = - 60 cm, f = + 20 cm$

$\frac{1}{v} - \frac{1}{u} = \frac{1}{f} gives v = + 30 cm 1 / 2$

For the convex mirror,

$\begin{matrix} u = + (30 - 15) cm = 15 cm, f = + \frac{20}{2} cm = 10 {cm}^{1 / 2} \frac{1}{v} + \frac{1}{u} = \frac{1}{f} gives v = + 30 cm \end{matrix}$

The final image is formed at the distance of $30 cm$ from the convex mirror (or $45 cm$ from the convex lens) to the right of the convex mirror.

AT Q. 8. A ray $P Q$ is incident normally on the face $A B$ of a triangular prism of refracting angle of $60^{\circ}$ , made of a transparent material of refractive index $\frac{2}{\sqrt{3}}$ , as shown in the figure. Trace the path of the ray as it passes through the prism. Also calculate the angle of emergence and angle of deviation.

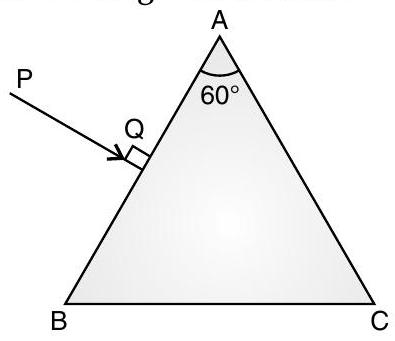
[Delhi Comptt. I, II, III 2014]

Ans. If $i_{c}$ is the critical angle for the prism/material,

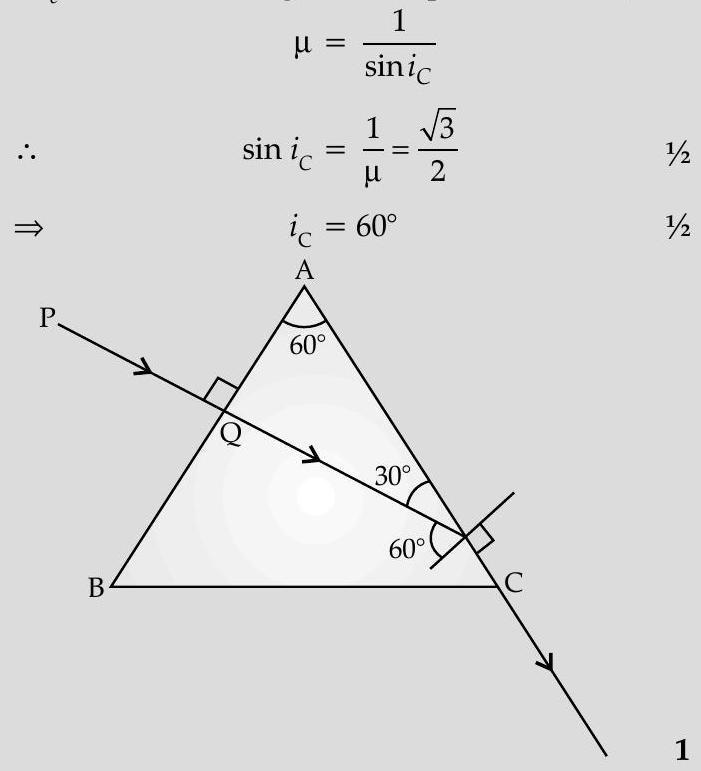
Angle of incidence at face $A C$ of the prism $= 60^{\circ} \frac{1}{2}$ Hence, refracted ray grazes the surface $A C$ .

$\Rightarrow$ Angle of emergence $= 90^{\circ}$

$1 / 2$

$\Rightarrow$ Angle of deviation $= 30^{\circ}$

[CBSE Marking Scheme 2014] 11/2

Ray Optics And Optical Instruments

ray-optics-and-optical-instruments Question 37

Detailed Answer :

Long Answer Type Questions

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Ray Optics And Optical Instruments

ray-optics-and-optical-instruments Question 37

Detailed Answer :

Long Answer Type Questions

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu