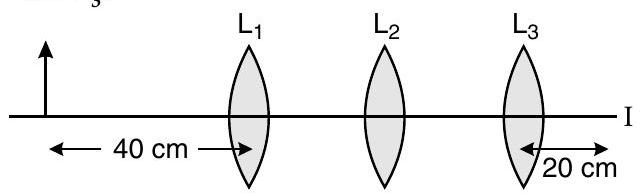
Question: Q. 6. You are given three lenses and each of focal length . An object is kept at in front of . The final real image is formed at the focus of . Find the separations between and .
[O.D. I, II, III 2012]
It shows that must render the rays parallel to the common axis. It means that the image , formed by , must be at a distance of from (at the focus of )
Therefore, distance between and and distance between and can have any value.
[CBSE Marking Scheme 2012] 1/22
Detailed Answer :
Given,
For lens,
( + ve sign shows it is right hand side of lens )
Now for , the final image is at its focus, that means . Hence
Now, since image of the object formed by convex lens is virtual object for , therefore .
Hence for lens and . Using the lens formula,
So, the separation between and
As and , therefore the distance between and does not matter it may take any value because image by is formed at infinity.
(AI Q. 7. A convex lens of focal length is placed coaxially with a convex mirror of radius of curvature . The two are kept at from each other. A point object lies in front of the convex lens. Draw a ray diagram to show the formation of the image by the combination. Determine the nature and position of the image formed. [O.D. I, II, III 2014]
Show Answer
Solution:
Ans.
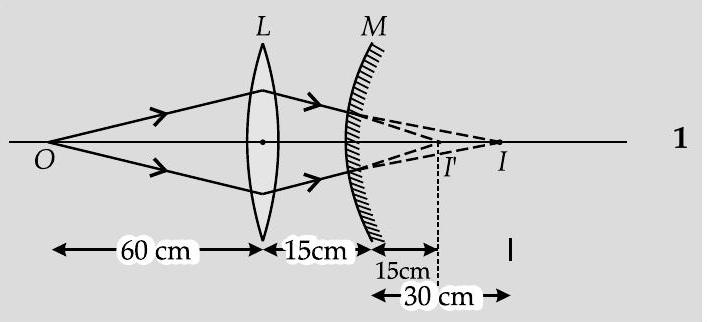
For the convex lens,
For the convex mirror,
The final image is formed at the distance of from the convex mirror (or from the convex lens) to the right of the convex mirror.
AT Q. 8. A ray is incident normally on the face of a triangular prism of refracting angle of , made of a transparent material of refractive index , as shown in the figure. Trace the path of the ray as it passes through the prism. Also calculate the angle of emergence and angle of deviation.
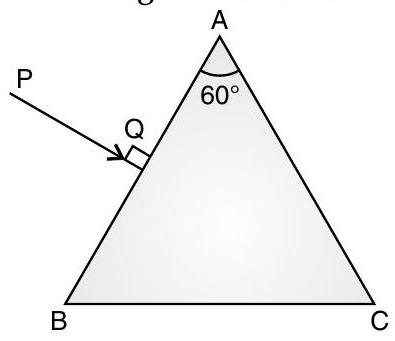
[Delhi Comptt. I, II, III 2014]
Ans. If is the critical angle for the prism/material,
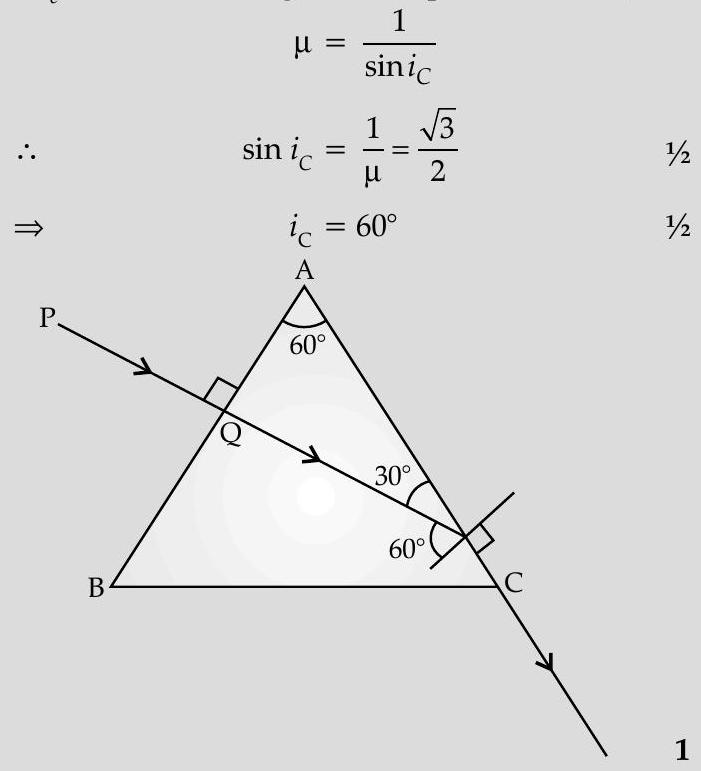
Angle of incidence at face of the prism Hence, refracted ray grazes the surface .
Angle of emergence
Angle of deviation
[CBSE Marking Scheme 2014] 11/2
Long Answer Type Questions










