SATHEE: ray-optics-and-optical-instruments Question 33

ray-optics-and-optical-instruments Question 33

Question: Q. 10. A ray of light, incident on an equilateral glass prism $(μ_{g} = \sqrt{3})$ moves parallel to the base line of the prism inside it. Find the angle of incidence for this ray.

A [Delhi I, II, III 2012]

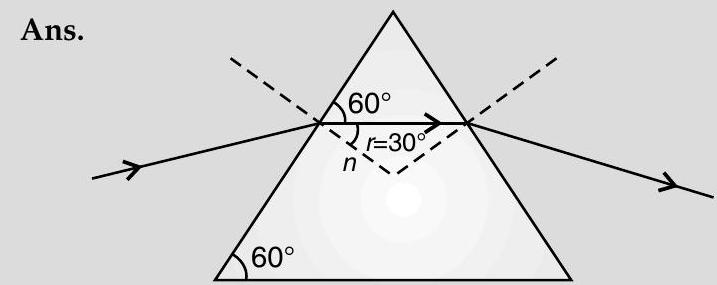
From the diagram, $r = 30^{\circ}$

Also

$n_{21} = \frac{\sin i}{\sin r}$

or,

$\sqrt{3} = \frac{\sin i}{\sin 30^{\circ}}$

or, $\sin i = \sqrt{3} \times \frac{1}{2}$

or, $i = 60^{\circ}$

[CBSE Marking Scheme 2012]

Short Answer Type Questions-II

(3 marks each)

Q. 1. (i) Show using a proper diagram how unpolarized light can be linearly polarised by reflection from a transparent glass surface.

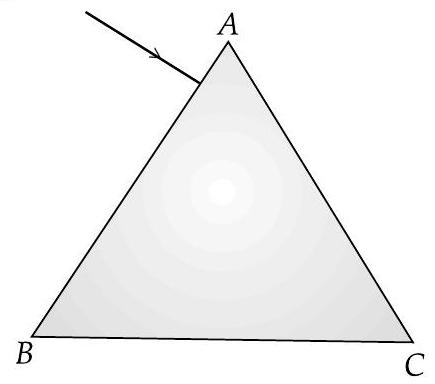
(ii) The figure shows a ray of light falling normally on on the face $A B$ of an equilateral glass prism having refractive index $\frac{3}{2}$ , placed in water of refractive index $\frac{4}{3}$ . Will this ray suffer total internal reflection on striking the face $A C$ ? Justify your answer.

A [CBSE 2018, 2012]

Show Answer

Solution:

Ans. (i) The diagram, showing polarisation by reflection is as shown. [Here the reflected and refracted rays are at right angle to each other.

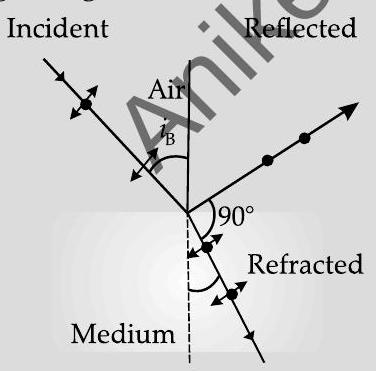
$\begin{array}{ll} ∴ & r = (\frac{π}{2} - i_{B}) ∴ & μ = (\frac{\sin i_{B}}{\sin r} = \tan i_{B}) \end{array}$

Thus light gets totally polarised by reflection when it is incident at an angle $i_{B}$ (Brewster’s angle), where $i_{B} = \tan^{- 1} μ$

(ii) The angle of incidence, of the ray, on striking the face $AC$ is $i = 60^{\circ}$ (as from figure)

Also, relative refractive index of glass, with respect to the surrounding water, is

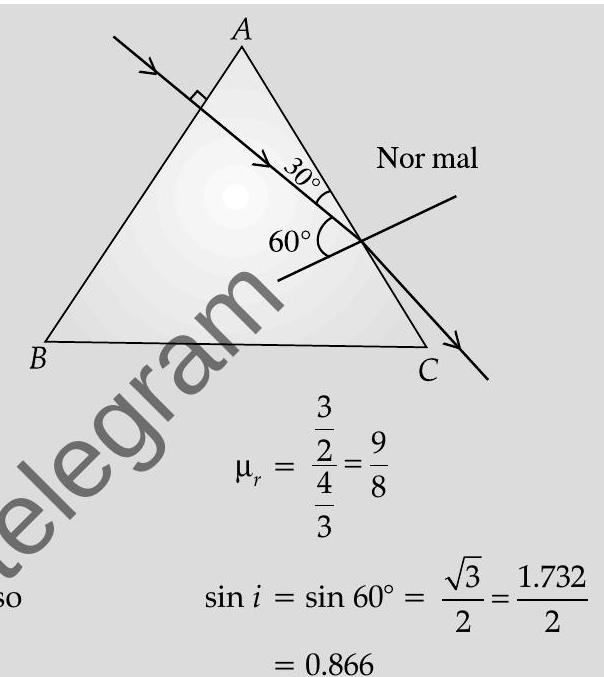
For total internal reflection, the required critical angle, in this case, is given by

$\sin i_{C} = \frac{1}{μ} = \frac{8}{9} ≃ 0.89$

$∴ i < i_{C}$

Hence the ray would not suffer total internal reflection on striking the face $A C$ .

[The student may just write the two conditions needed for total internal reflection without analysis of the given case.

The student may be awarded $(1 / 2 + 1 / 2)$ mark in such a case.

[CBSE Marking Scheme 2018]

AT Q. 2. (i) Monochromatic light of wavelength $589 nm$ is incident from air on a water surface. If $μ$ for water is 1.33 , find the wavelength, frequency and speed of the refracted light.

(ii) A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is $20 cm$ .

U [OD I, II, III, 2016]

Ans. (i)

$λ = \frac{589 nm}{1 \cdot 33} = 442 \cdot 8 nm 1 / 2$

Frequency,

$v = \frac{3 \times 10^{8} {ms}^{- 1}}{589 nm}$

$= 5.09 \times 10^{14} Hz$

$1 / 2$

Speed

$v = \frac{3 \times 10^{8}}{1.33} m / s$

(ii)

$\begin{aligned} = 2 \cdot 25 \times 10^{8} m / s & \frac{1}{f} = [\frac{μ_{2}}{μ_{1}} - 1] [\frac{1}{R_{1}} - \frac{1}{R_{2}}] & \frac{1}{20} = [\frac{1.55}{1} - 1] \frac{2}{R} & R = (20 \times 1 \cdot 10) cm = - 22 cm & 1 / 2 \end{aligned}$

$∴ \frac{1}{20} = [\frac{1.55}{1} - 1] \frac{2}{R}$

$∴ R = (20 \times 1 \cdot 10) cm = - 22 cm$

[CBSE Marking Scheme 2016]

Ray Optics And Optical Instruments

ray-optics-and-optical-instruments Question 33

Short Answer Type Questions-II

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Ray Optics And Optical Instruments

ray-optics-and-optical-instruments Question 33

Short Answer Type Questions-II

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu