SATHEE: moving-charges-and-magnetism Question 43

moving-charges-and-magnetism Question 43

Question: Q. 2. An electron of mass $m_{e}$ revolves around a nucleus of charge $+ Z_{e}$ . Show that it behaves like a tiny magnetic dipole. Hence, prove that the magnetic moment associated with it is expressed as $\vec{μ} = - \frac{e}{2 m_{e}} \vec{L}$ , where $\vec{L}$ is the orbital angular momentum of the electron. Give the significance of negative sign.

U [Delhi II 2017]

Show Answer

Solution:

Ans. (i) Behaviour of revolving electron as a tiny magnetic dipole.

(ii) Proof of the relation, $\vec{μ} = - \frac{e}{2 m_{e}} \vec{L}$

(iii) Significance of negative sign

Electron, in circular motion around the nucleus constitutes a current loop which behaves like a magnetic dipole.

Current associated with the revolving electron

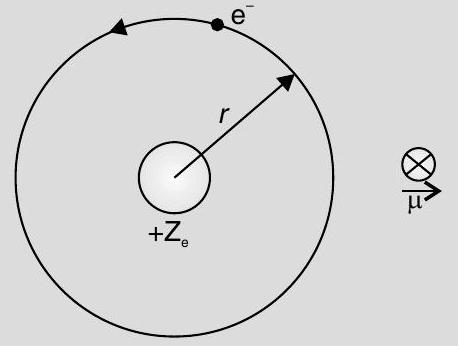
$\begin{aligned} I & = \frac{e}{T} and T & = \frac{2 π r}{v} ∴ I & = \frac{- e}{2 π r} v \end{aligned}$

Magnetic moment of the loop,

$\begin{aligned} μ & = I A μ & = I A = \frac{- e v}{2 π r} π r^{2} & = \frac{- e v r}{2} = \frac{- e \cdot m_{e} v r}{2 m_{e}} \end{aligned}$

Orbital angular momentum of the electron,

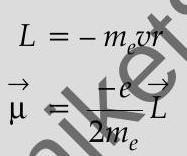
-ve sign signifies that the angular momentum of the revolving electron is opposite in direction to the magnetic moment associated with it.

[CBSE Marking Scheme 2017]

[AI Q. 3. Define the term current sensitivity of a galvanometer. In the circuits shown in the figures, the galvanometer shows no deflection in each case. Find the ratio of 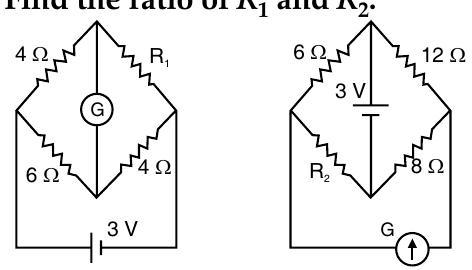$R_{1}$ and $R_{2}$ .

U] [O.D. Comptt I, III 2017]

Ans. Definition of current sensitivity

Ratio $\frac{R_{1}}{R_{2}}$

Current sensitivity of a galvanometer is deflection per unit current

$\begin{array}{ll} [Alternatively, I_{s} = \frac{θ}{I} = \frac{N A B}{K}] In circuit (i), \frac{4}{6} = \frac{R_{1}}{4} \Rightarrow R_{1} = \frac{8}{3} Ω In circuit (ii), \frac{6}{R_{2}} = \frac{12}{8} \Rightarrow R_{2} = 4 Ω ∴ \frac{R_{1}}{R_{2}} = \frac{2}{3} \end{array}$

[CBSE Marking Scheme 2017]

Detailed Answer :

(i) Current sensitivity of galvanometer is the deflection produced when unit current passes through the galvanometer. A galvanometer is said to be sensitive if it produces large deflection for a small current.

$I = \frac{C}{n B A} θ$

where, $C$ is torsional constant.

$Currentsensitivity = \frac{θ}{I} = \frac{n B A}{C}$

(ii) Consider the circuit I :

For balanced Wheatstone bridge, there will be no deflection in the galvanometer, so

Hence,

$\begin{aligned} \frac{4}{R_{1}} & = \frac{6}{4} R_{1} & = \frac{4 \times 4}{6} = \frac{8}{3} Ω \end{aligned}$

$1 / 2$

Consider the circuit II :

For equivalent circuit, when the Wheatstone bridge is balanced, there will be no deflection in the galvanometer, so

Hence,

$\frac{6}{12} = \frac{R_{2}}{8}$

$R_{2} = \frac{6 \times 8}{12} = 4 Ω$

Now ratio,

$\begin{matrix} (1) & ∴ \frac{R_{1}}{R_{2}} = \frac{\frac{8}{3}}{4} = \frac{2}{3} \end{matrix}$

Moving Charges And Magnetism

moving-charges-and-magnetism Question 43

Detailed Answer :

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Moving Charges And Magnetism

moving-charges-and-magnetism Question 43

Detailed Answer :

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu