Question: Q. 2. An electron of mass
U [Delhi II 2017]
Show Answer
Solution:
Ans. (i) Behaviour of revolving electron as a tiny magnetic dipole.
(ii) Proof of the relation,
(iii) Significance of negative sign
Electron, in circular motion around the nucleus constitutes a current loop which behaves like a magnetic dipole.
Current associated with the revolving electron
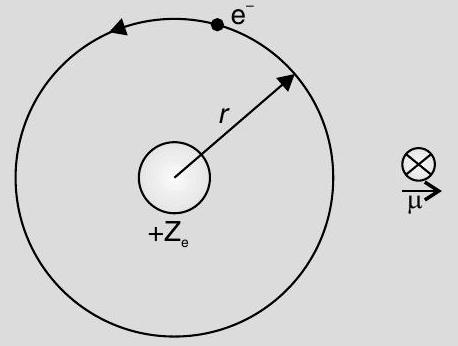
Magnetic moment of the loop,
Orbital angular momentum of the electron,
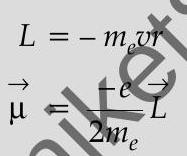
-ve sign signifies that the angular momentum of the revolving electron is opposite in direction to the magnetic moment associated with it.
[CBSE Marking Scheme 2017]
[AI Q. 3. Define the term current sensitivity of a galvanometer. In the circuits shown in the figures, the galvanometer shows no deflection in each case. Find the ratio of 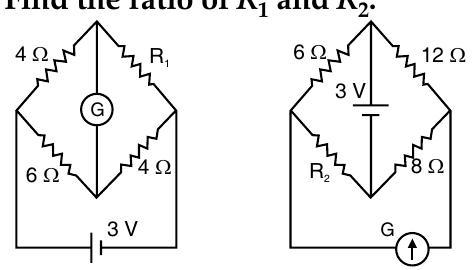
U] [O.D. Comptt I, III 2017]
Ans. Definition of current sensitivity
Ratio
Current sensitivity of a galvanometer is deflection per unit current
[CBSE Marking Scheme 2017]
Detailed Answer :
(i) Current sensitivity of galvanometer is the deflection produced when unit current passes through the galvanometer. A galvanometer is said to be sensitive if it produces large deflection for a small current.
where,
(ii) Consider the circuit I :
For balanced Wheatstone bridge, there will be no deflection in the galvanometer, so
Hence,
Consider the circuit II :
For equivalent circuit, when the Wheatstone bridge is balanced, there will be no deflection in the galvanometer, so
Hence,
Now ratio,






