Solution:

Ans. (i) Derivation of the expression for cyclotron frequency

2

(ii) Reason/justification for the correct answer 1

(i)

$$ \begin{array}{rlrl} \frac{m v^{2}}{r} & =q v B & 1 / 2 \ r & =\frac{m v}{q B} & 1 / 2 \end{array} $$

Frequency of revolution, $v=\frac{1}{\text { Time Period }}$

$$ =\frac{v}{2 \pi r}=\frac{q B}{2 \pi m} \quad \mathbf{1} $$

(ii) No

The mass of the two particles, i.e., deuteron and proton, is different.

Since (cyclotron) frequency depends inversely on the mass, they cannot be accelerated by the same oscillator frequency.

[CBSE Marking Scheme 2017]

Detailed Answer :

i) Let a particle of charge $q$ revolving in the path of radius $r$ with velocity $v$, so for circular motion,

Centripetal force $=$ Lorentz force (due to magnetic field $B$ )

$$ \frac{m v^{2}}{r}=q v \mathrm{~B} $$

$1 / 2$

Now,

$$ \begin{equation*} \frac{v}{r}=\frac{q B}{m} \tag{i} \end{equation*} $$

But, angular velocity, $\omega=\frac{v}{r}$

Hence,

$$ \begin{equation*} \omega=\frac{q B}{m} \tag{ii} \end{equation*} $$

Using Time period, $\mathrm{T}=\frac{2 \pi}{\omega}$

equation (ii), can be written as,

$$ \mathrm{T}=\frac{2 \pi m}{q B} $$

Cyclotron frequency, $n=\frac{1}{T}=\frac{\omega}{2 \pi}=\frac{q B}{2 \pi m}$

(ii) A cyclotron works only when the frequency of the revolution of particle is equal to the frequency of oscillation.

$\therefore$ Mass of proton and deuteron are different

$$ \begin{array}{rr} \text { i.e., } & \left(m_{d}=2 m_{p}\right) \ \text { and } & v \propto \frac{1}{m} \end{array} $$

$\therefore$ Frequency of revolution of proton and deuteron is different, so they can’t be accelerated with same oscillator frequency.

AI Q. 14. (i) Name the machine which uses crossed electric and magnetic fields to accelerate the ions to high energies. With the help of a diagram, explain the resonance condition.

(ii) What will happen to the motion of charged particle if the frequency of the alternating voltage is doubled?

R [CBSE SQP 2016]

OR

Draw a schematic sketch of a cyclotron. Explain, giving the essential details of its construction, how it is used to accelerate the charged particles.

[O.D., Delhi I, II, III 2014, 2011]

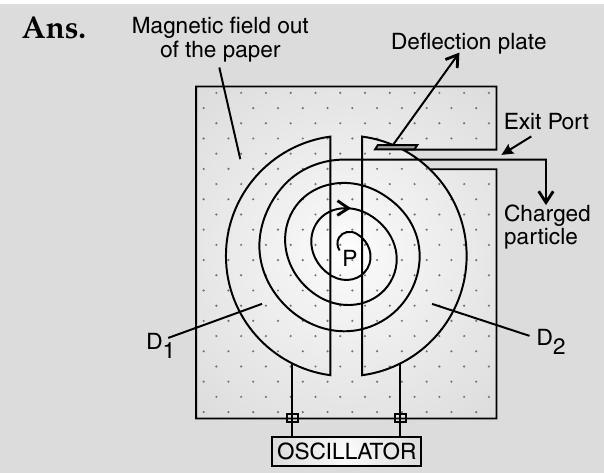
Construction : The cyclotron is made up of two hollow semi-circular discs like metal containers, $D_{1}$ and $D_{2}$ called dees.

It uses crossed electric and magnetic fields. The electric field is provided by an oscillator of adjustable frequency.

Working : In a cyclotron, the frequency of the applied alternating field is adjusted tobe equal to the frequency of revolution of the charged particles in the magnetic field. This ensures that the particles get accelerated every time, they cross the space between the two dees. The radius of their path increases with increase in energy and they are finally made to leave the system via an exit slit. (ii) (a) Particle will accelerate and deaccelerate alternately. However, the radius of path remain unchanged.

1

[CBSE Marking Scheme 2011]