Question: Q. 13. (i) Obtain an expression for cyclotron frequency.
(ii) A deuteron and a proton are accelerated by the cyclotron. Can both be accelerated with the same oscillator frequency? Give reason to justify your answer.
U] [Delhi Set I, II, III 2017]
Show Answer
Solution:
Ans. (i) Derivation of the expression for cyclotron frequency
2
(ii) Reason/justification for the correct answer 1
(i)
Frequency of revolution,
(ii) No
The mass of the two particles, i.e., deuteron and proton, is different.
Since (cyclotron) frequency depends inversely on the mass, they cannot be accelerated by the same oscillator frequency.
[CBSE Marking Scheme 2017]
Detailed Answer :
i) Let a particle of charge
Centripetal force
Now,
But, angular velocity,
Hence,
Using Time period,
equation (ii), can be written as,
Cyclotron frequency,
(ii) A cyclotron works only when the frequency of the revolution of particle is equal to the frequency of oscillation.
AI Q. 14. (i) Name the machine which uses crossed electric and magnetic fields to accelerate the ions to high energies. With the help of a diagram, explain the resonance condition.
(ii) What will happen to the motion of charged particle if the frequency of the alternating voltage is doubled?
R [CBSE SQP 2016]
OR
Draw a schematic sketch of a cyclotron. Explain, giving the essential details of its construction, how it is used to accelerate the charged particles.
[O.D., Delhi I, II, III 2014, 2011]
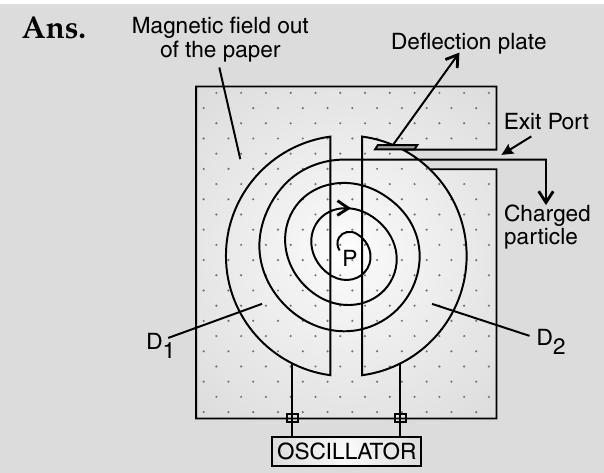
Construction : The cyclotron is made up of two hollow semi-circular discs like metal containers,
It uses crossed electric and magnetic fields. The electric field is provided by an oscillator of adjustable frequency.
Working : In a cyclotron, the frequency of the applied alternating field is adjusted tobe equal to the frequency of revolution of the charged particles in the magnetic field. This ensures that the particles get accelerated every time, they cross the space between the two dees. The radius of their path increases with increase in energy and they are finally made to leave the system via an exit slit. (ii) (a) Particle will accelerate and deaccelerate alternately. However, the radius of path remain unchanged.
1
[CBSE Marking Scheme 2011]






