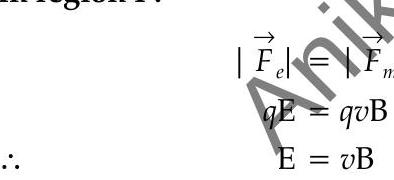Question: Q. 12. A fine pencil of -particles moving with a speed, enters a region (region ), where a uniform electric and a uniform magnetic fields are both present. These -particles then move into region II where only the magnetic field, (out of the two fields present in region ), exists. The path of the -particles in the two regions is as shown in the figure.
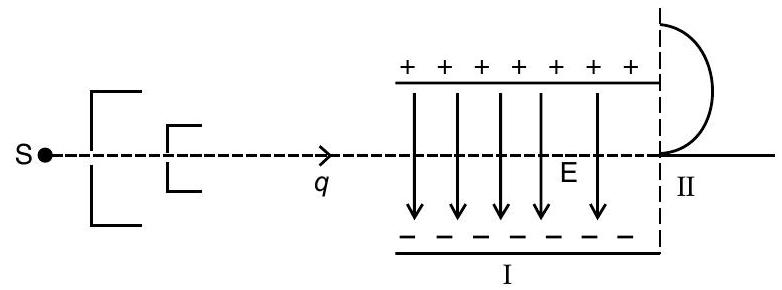
(i) State the direction of the magnetic field.
(ii) State the relation between ’ ’ and ’ ’ in region I.
(iii) Derive the expression for the radius of the circular path of the -particle in region II.
If the magnitude of magnetic field in region is changed to times its earlier value (without changing the magnetic field in region I), find the factor by which the radius of this circular path would change.
A&E [CBSE SQP 2013]
Show Answer
Solution:
Ans. (i) The magnetic field is perpendiculan to the plane of paper and is directed inward
(ii) In region I :
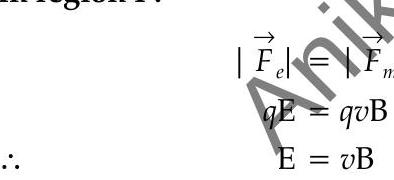
(iii) In region II :
Substituting the value of , we get
Let denote the new magnetic field in region II. If is the radius of the circular path now, we have
Hence, radius of the circular path, would decrease by a factor .