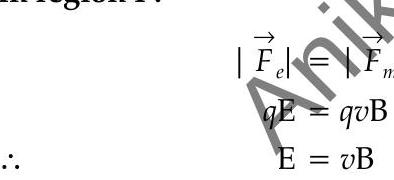Question: Q. 12. A fine pencil of $\beta$-particles moving with a speed, enters a region (region $I$ ), where a uniform electric and a uniform magnetic fields are both present. These $\beta$-particles then move into region II where only the magnetic field, (out of the two fields present in region $I$ ), exists. The path of the $\beta$-particles in the two regions is as shown in the figure.
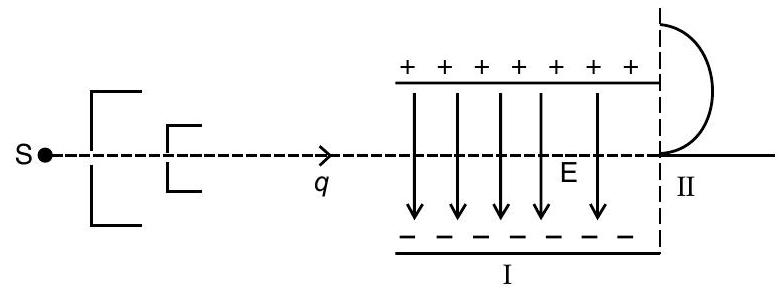
(i) State the direction of the magnetic field.
(ii) State the relation between ’ $E$ ’ and ’ $B$ ’ in region I.
(iii) Derive the expression for the radius of the circular path of the $\beta$-particle in region II.
If the magnitude of magnetic field in region $U$ is changed to $n$ times its earlier value (without changing the magnetic field in region I), find the factor by which the radius of this circular path would change.
A&E [CBSE SQP 2013]
Show Answer
Solution:
Ans. (i) The magnetic field is perpendiculan to the plane of paper and is directed inward
(ii) In region I :
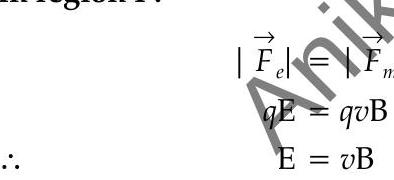
(iii) In region II :
$$ \begin{aligned} \frac{m v^{2}}{r} & =q v \mathrm{~B} \ \Rightarrow \quad r & =\frac{m v}{q \mathrm{~B}} \end{aligned} $$
Substituting the value of $v$, we get
$$ r=\frac{m E}{q B^{2}} $$
Let $\mathrm{B}^{\prime}(=n \mathrm{~B})$ denote the new magnetic field in region II. If $r^{\prime}$ is the radius of the circular path now, we have
$$ r^{\prime}=\frac{m \mathrm{E}}{q \mathrm{~B}^{\prime 2}}=\frac{m \mathrm{E}}{q n^{2} \mathrm{~B}^{2}} $$
Hence, radius of the circular path, would decrease by a factor $n^{2}$.
