Solution:

Ans. Equivalent capacitance in series

Energy in series combination $1/2$

Charge in series combination $1/2$

Equivalent capacitance in parallel combination $1/2$

Energy in parallel combination $1/2$ Charge in parallel combination $1/2$

In series combination :

$$\frac{1}{C_s}=(\frac{1}{12}+\frac{1}{12})(pF{)}^{-1}1/2$$

$\therefore C_{\mathrm{s}}=6\times {10}^{-12}\mathrm{F}$

$U_{\mathrm{s}}=\frac{1}{2}{\mathrm{CV}}^2$

$U_{\mathrm{s}}=\frac{1}{2}\times 6\times {10}^{-12}\times 50\times 50\mathrm{J}$

$$\begin{array}{rlr}{U}_{\mathrm{s}}& =75\times {10}^{-10}\mathrm{J}{q}_{\mathrm{s}}& =C_{\mathrm{s}}V\end{array}$$

$$=6\times {10}^{-12}\times 50\mathrm{C}$$

$$\begin{array}{rlr}& =300\times {10}^{-12}\mathrm{C}& =3\times {10}^{-10}\mathrm{C}\end{array}$$

$1/2$

In parallel combination :

$$\begin{array}{rlrlrlrl}{C}_p& =(12+12)p\mathrm{F}{C}_p& =24\times {10}^{-12}\mathrm{F}{U}_p& =\frac{1}{2}\times 24\times {10}^{-12}\times 2500\mathrm{J}{U}_p& =3\times {10}^{-8}\mathrm{J}{q}_p& =C_{p}V& =24\times {10}^{-12}\times 50\mathrm{C}& =1.2\times {10}^{-9}\mathrm{C}\end{array}$$

$$\therefore C_p=24\times {10}^{-12}\mathrm{F}$$

[CBSE Marking Scheme 2017]

13. Two identical parallel plate capacitors $A$ and $B$ are connected to a battery of $V$ volts with the switch $S$ closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant $\kappa$. Find the ratio of the total electrostatic energy stored in bothcapacitors before and after the introduction of the dielectric.

[Topper’s Answers 2017]

[AI Q. 14. Two parallel plate capacitors $X$ and $Y$ have the same area of plates and same separation between them. $X$ has air between the plates while $Y$ contains a dielectric medium of ${\epsilon }_r=4$.

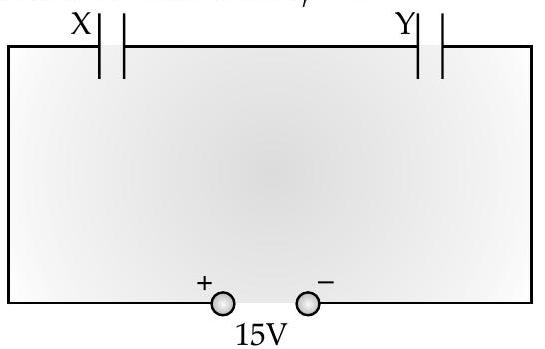
(i) Calculate capacitance of each capaciton i equivalent capacitance of the combination is $4\mu \mathrm{F}$.

(ii) Calculate the potential difference between the plates of $X$ and $Y$.

(iii) Estimate the ratio of electrostaticengy stored in $X$ and $Y$.

U] [Delhi I, II, III 2016, Set D, 2009, Set F 2008]

Ans. (i) Let

$$\begin{array}{rlr}& C_X=C& C_Y=4C\end{array}$$

(as it has a dielectricmedium of ${\epsilon }_r=4$ )

For series combination of two capacitors

$$\frac{1}{C}=\frac{1}{C_X}+\frac{1}{C_Y}$$

$\Rightarrow \frac{1}{4\mu \mathrm{F}}=\frac{1}{\mathrm{C}}+\frac{1}{4\mathrm{C}}$

$$\frac{1}{4\mu \mathrm{F}}=\frac{5}{4\mathrm{C}}$$

$\Rightarrow C=5\mu \mathrm{F}$

Hence $C_X=5\mu \mathrm{F}$

(ii) Total charge

$$C_Y=20\mu \mathrm{F}$$

$$\begin{array}{rlr}& =4\mu \mathrm{F}\times 15\mathrm{V}=60\mu \mathrm{C}{V}_X& =\frac{Q}{C_X}=\frac{60\mu \mathrm{C}}{5\mu \mathrm{F}}=12\mathrm{V}\end{array}$$

$$V_Y=\frac{Q}{C_Y}=\frac{60\mu \mathrm{C}}{20\mu \mathrm{F}}=3\mathrm{V}$$

(iii)

$$=\frac{\overline{2C_X}}{\frac{Q^2}{2C_x}}=\frac{C_Y}{C_X}=\frac{20}{5}=4:1\mathbf{1}$$

(Also accept any other correct alternative method)

[CBSE Marking Scheme 2016]

. A parallel plate capacitor, of capacitance $20\mu \mathrm{F}$, is connected to a $100\mathrm{V}$, supply. After sometime, the battery is disconnected, and the space, between the plates of the capacitor is filled with a dielectric of dielectric constant 5 . Calculate the energy stored in the capacitor.

(i) Before

(ii) After the dielectric has been put in between its plates.

A [O.D. Comptt. I, II, III, 2016]

Ans. Charge stored, $Q=CV=20\times {10}^{-6}\times 100\mathrm{C}1/2$

$$=2000\mu \mathrm{C}$$

New value of capacitance

$$\begin{array}{rlr}& =5\times 20\mu \mathrm{F}& =100\mu \mathrm{F}\end{array}$$

Energy stored in a capacitor

$$=\frac{1}{2}\frac{Q^2}{C}(=\frac{1}{2}C{V}^2=\frac{1}{2}QV)1/2$$

(i) Energy stored before dielectric

$$\begin{array}{}\text{(1)}& & =\frac{1}{2}\times \frac{[2000\times {10}^{-6}]\times (2000\times {10}^{-6})}{20\times {10}^{-6}}& =0.1\mathrm{J}\end{array}$$

(ii) Energy stored after the dielectric is introduced ( $\because$ there is no change in the value of $Q$ )

$$\begin{array}{rlrl}& =\frac{1}{2}\times \frac{2000\times {10}^{-6}\times 2000\times {10}^{-6}}{100\times {10}^{-6}}1/2& =0.02\mathrm{J}& 1/2\end{array}$$

[CBSE Marking Scheme, 2016]