Question: Q. 12. Two identical capacitors of
Also find the charge drawn from the battery in each case.
U] [Delhi III 2017]
Show Answer
Solution:
Ans. Equivalent capacitance in series
Energy in series combination
Charge in series combination
Equivalent capacitance in parallel combination
Energy in parallel combination
In series combination :
In parallel combination :
[CBSE Marking Scheme 2017]
- Two identical parallel plate capacitors


[Topper’s Answers 2017]
[AI Q. 14. Two parallel plate capacitors
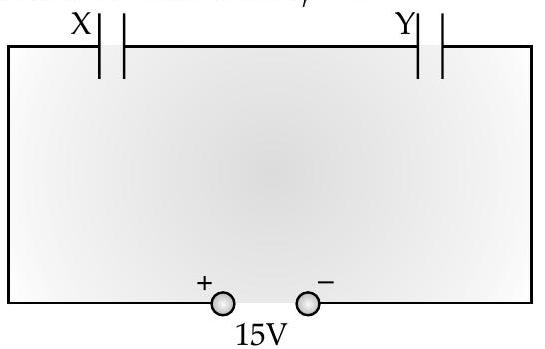
(i) Calculate capacitance of each capaciton i equivalent capacitance of the combination is
(ii) Calculate the potential difference between the plates of
(iii) Estimate the ratio of electrostaticengy stored in
U] [Delhi I, II, III 2016, Set D, 2009, Set F 2008]
Ans. (i) Let
(as it has a dielectricmedium of
For series combination of two capacitors
Hence
(ii) Total charge
(iii)
(Also accept any other correct alternative method)
[CBSE Marking Scheme 2016]
. A parallel plate capacitor, of capacitance
(i) Before
(ii) After the dielectric has been put in between its plates.
A [O.D. Comptt. I, II, III, 2016]
Ans. Charge stored,
New value of capacitance
Energy stored in a capacitor
(i) Energy stored before dielectric
(ii) Energy stored after the dielectric is introduced (
[CBSE Marking Scheme, 2016]






