electromagnetic-induction Question 2
Question: Q. 2. A loop, made of straight edges has six corners at $A(0,0,0), B(L, 0,0) C(L, L, 0), D(0, L, 0), E(0, L, L)$ and $F(0,0, L)$. A magnetic field $\vec{B}=B_{0}(\hat{i}+\hat{k})$ Tesla is present in the region. The flux passing through the loop $A B C D E F A$ (in that order) is (a) $B_{0} L^{2} \mathrm{~Wb}$. (b) $2 B_{0} L^{2} \mathrm{~Wb}$. (c) $\sqrt{2} B_{0} L^{2} W b$. (d) $4 B_{0} L^{2} \mathrm{~Wb}$.
[NCERT Exemplar]
Show Answer
Solution:
Ans. Correct option : (b)
Explanation: The loop can be considered in two planes :
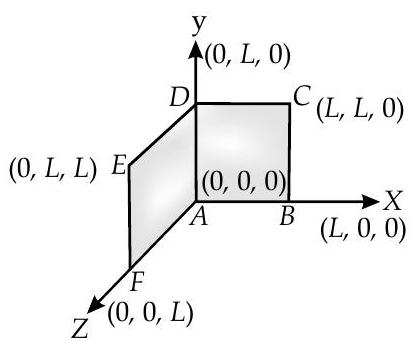
(i) Plane of $A B C D A$ is in $X-Y$ plane. So its vector $\vec{A}$ is in Z-direction. Hence,
$$ A_{1}=|A| \hat{k}=L^{2} \hat{k} $$
(ii) Plane of $D E F A D$ is in $Y$-Z plane
$$ \begin{aligned} & \text { So } A_{2}=|A| \hat{i}=L^{2} \hat{i} \ & \therefore \quad A=A_{1}+A_{2}=L^{2}(\hat{i}+\hat{k}) \ & B=\mathrm{B}{0}(\hat{i}+\hat{k}) \ & \text { So, } Q=B . A \ & =\mathrm{B}{0}(\hat{i}+\hat{k}) \cdot L^{2}(\hat{i}+\hat{k}) \ & =B_{0} L^{2} \ & =B_{0} L^{2}[1+0+0+1] \ & =2 B_{0} L^{2} W b \end{aligned} $$
