Question: Q. 2. A loop, made of straight edges has six corners at
[NCERT Exemplar]
Show Answer
Solution:
Ans. Correct option : (b)
Explanation: The loop can be considered in two planes :
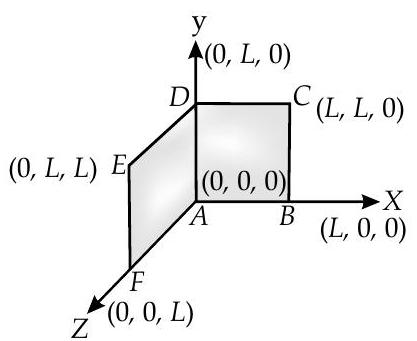
(i) Plane of
(ii) Plane of
$$ \begin{aligned} & \text { So } A_{2}=|A| \hat{i}=L^{2} \hat{i} \ & \therefore \quad A=A_{1}+A_{2}=L^{2}(\hat{i}+\hat{k}) \ & B=\mathrm{B}{0}(\hat{i}+\hat{k}) \ & \text { So, } Q=B . A \ & =\mathrm{B}{0}(\hat{i}+\hat{k}) \cdot L^{2}(\hat{i}+\hat{k}) \ & =B_{0} L^{2} \ & =B_{0} L^{2}[1+0+0+1] \ & =2 B_{0} L^{2} W b \end{aligned} $$






