Solution:

Ans. (i) Derivation of the expression for electric field $\vec{E}$

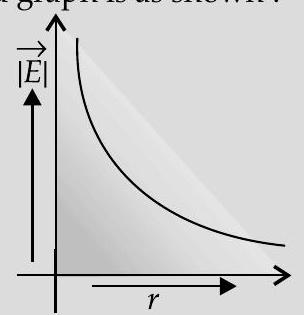
(ii) Graph to show the required variation of the electric field

(iii) Calculation of work done 1

(i)

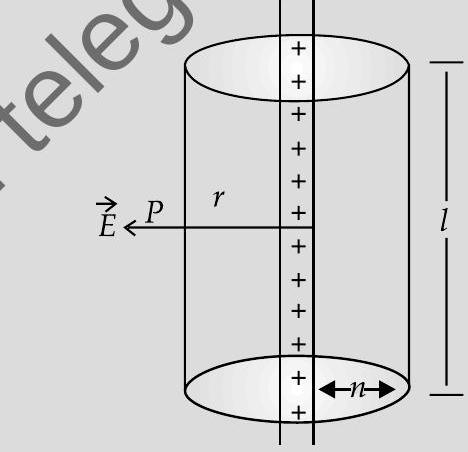
To calculate the electric field, imagine a cylindrical Gaussian surface, since the field is everywhere radial, flux through two ends of the cylindrical Gaussian surface is zero.

$1 / 2$

At cylindrical part of the surface electric field $\overrightarrow{\boldsymbol{E}}$ is normal to the surface at every point and its magnitude is constant.

Therefore flux through the Gaussian surface $=$ Flux through the curved cylindrical part of the surface,

$$ \begin{equation*} =\mathrm{E} \times 2 \pi r l \tag{i} \end{equation*} $$

Applying Gauss’s Law

Flux,

$$ \phi=\frac{q_{\text {enclosed }}}{\varepsilon_{0}} $$

Total charge enclosed $=$ Linear charge density $\times l$

$$ \begin{align*} & =\lambda l \ \phi & =\frac{\lambda l}{\varepsilon_{0}} \tag{ii} \end{align*} $$

Using Equations (i) & (ii)

$$ \begin{aligned} E \times 2 \pi r l & =\frac{\lambda l}{\varepsilon_{0}} \ \Rightarrow \quad & E=\frac{\lambda}{2 \pi \varepsilon_{0} r} \end{aligned} $$

In vector notation, $\vec{E}=\frac{\lambda}{2 \pi \varepsilon_{0} r} \hat{n}$

(where $\hat{n}$ is a unit vector normal to the line charge) (ii) The required graph is as shown :

(iii) Work done in moving the charge ’ $q$ ’ through a small displacement ’ $d r$ '

$$ \begin{align*} d W & =\vec{F} \cdot \overrightarrow{d r} \ d W & =q \vec{E} \cdot \overrightarrow{d r} \ & =q E d r \cos 0 \ d W & =q \times \frac{\lambda}{2 \pi \varepsilon_{0} r} d r \end{align*} $$

Work done in moving the given charge from $r_{1}$ to $r_{2}$ $\left(r_{2}>r_{1}\right)$

$$ \begin{aligned} & W=\int_{r_{1}}^{r_{2}} d W=\int_{r_{1}}^{r_{2}} \frac{\lambda g d r}{2 \pi \varepsilon_{0} r} \ & W=\frac{\lambda q}{2 \pi \varepsilon_{0}}\left[\log {e} r{2}-\log {e} r{1}\right] \quad 1 / 2 \ & W=\frac{\lambda q}{2 \pi \varepsilon_{0}}\left[\log {e} \frac{r{2}}{r_{1}}\right] \end{aligned} $$

[CBSE Marking Scheme, 2018]