Question: Q. 2. (i) Use Gauss’ law to derive the expression for the electric field
(ii) Draw a graph to show the variation of
(iii) Find the work done in bringing a charge
Show Answer
Solution:
Ans. (i) Derivation of the expression for electric field
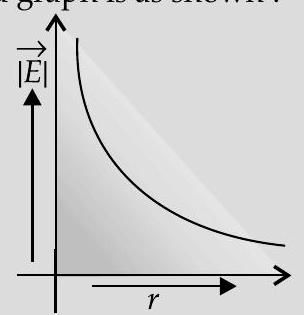
(ii) Graph to show the required variation of the electric field
(iii) Calculation of work done 1
(i)
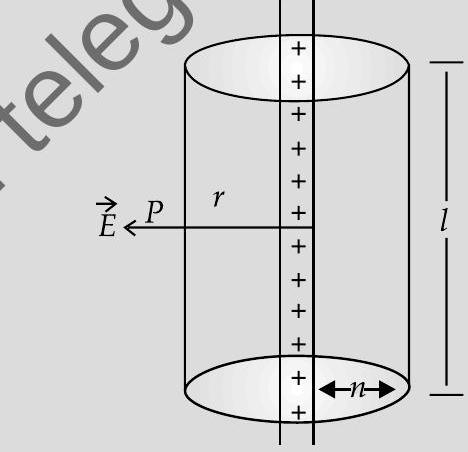
To calculate the electric field, imagine a cylindrical Gaussian surface, since the field is everywhere radial, flux through two ends of the cylindrical Gaussian surface is zero.
At cylindrical part of the surface electric field
Therefore flux through the Gaussian surface
Applying Gauss’s Law
Flux,
Total charge enclosed
Using Equations (i) & (ii)
In vector notation,
(where
(iii) Work done in moving the charge ’
Work done in moving the given charge from
$$ \begin{aligned} & W=\int_{r_{1}}^{r_{2}} d W=\int_{r_{1}}^{r_{2}} \frac{\lambda g d r}{2 \pi \varepsilon_{0} r} \ & W=\frac{\lambda q}{2 \pi \varepsilon_{0}}\left[\log {e} r{2}-\log {e} r{1}\right] \quad 1 / 2 \ & W=\frac{\lambda q}{2 \pi \varepsilon_{0}}\left[\log {e} \frac{r{2}}{r_{1}}\right] \end{aligned} $$
[CBSE Marking Scheme, 2018]






