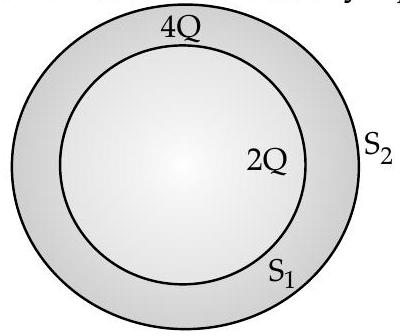
SATHEE: electric-charges-and-fields Question 51

electric-charges-and-fields Question 51

Question: Q. 10. Consider two hollow concentric spheres, $S_{1}$ and $S_{2}$ enclosing charges $2 Q$ and $4 Q$ respectively as shown in the figure. (i) Find out the ratio of the electric flux through them. (ii) How will the electric flux through the sphere $S_{1}$ change if a medium of dielectric constant ’ $ε_{r}$ ’ is introduced in the space inside $S_{1}$ in place of air ? Deduce the necessary expression.

[O.D. I, II, III 2014]

Show Answer

Solution:

Ans. According to the Gauss’s law,

$1 / 2$

$ϕ = \oint \vec{E} \cdot \vec{d S} = \frac{q_{enclosed}}{ε_{0}}$ $∴$ Forsphere $S_{1}$ , flux enclosed $= ϕ_{1} = \frac{2 Q}{ε_{0}} 1 / 2$ nd for sphere $S_{2}$ , flux enclosed $= ϕ_{2} = \frac{2 Q + 4 Q}{ε_{0}}_{1 / 2}$

$\begin{aligned} ϕ_{2} & = \frac{6 Q}{ε_{0}} \frac{ϕ_{1}}{ϕ_{2}} & = \frac{1}{3} \end{aligned}$

$1 / 2$

When a medium of dielectric constant $ε_{r}$ is introduced in the space inside sphere $S_{1}$ , the flux through $S_{1}$ would be $ϕ_{1}^{'} = \frac{2 Q}{ε_{r}}$ .

[CBSE Marking Scheme, 2014]

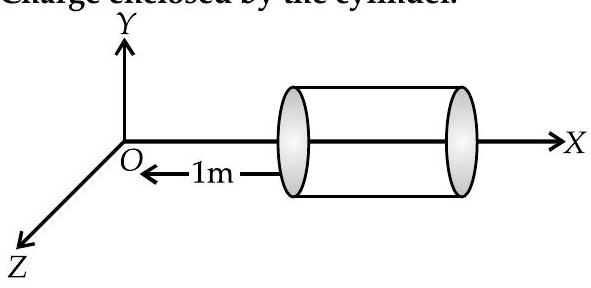
AI Q. 11. A hollow cylindrical box of length $1 m$ and area of cross-section $25 {cm}^{2}$ is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by $\vec{E} = 50 x \hat{i}$ , where $E$ is in ${NC}^{- 1}$ and $x$ is in metres. Find

(i) Net flux through the cylinder.

(ii) Charge enclosed by the cylinder.

A&E [Delhi I, II, III 2013]

Ans. (i) Given : $\vec{E} = 50 x \hat{i}$ and $Δ S = 25 {cm}^{2}$ or $25 \times 10^{- 4} m^{2}$

As the electric field is only along the $x$ -axis, hence, flux will pass only through the cross-section of cylinder.

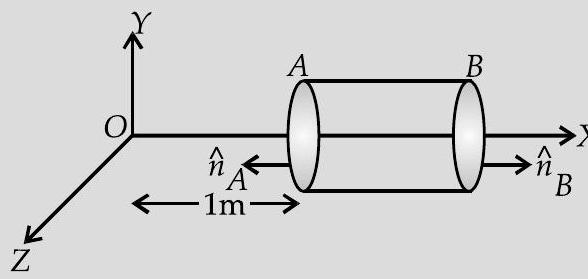
Magnitude of electric field at cross-section $A$ ,

$E_{A} = 50 \times 1 = 50 N / C .$

Magnitude of electric field at cross-section $B$ ,

$E_{B} = 50 \times 2 = 100 N / C$

The corresponding electric fluxes are

$\begin{aligned} \oint ϕ_{A} & = \vec{E} \cdot \vec{Δ S} & = 50 \times 25 \times 10^{- 4} \times \cos 180^{\circ} & = - 0.125 {Nm}^{2} / C^{2} \oint ϕ_{B} & = \vec{E} \cdot \vec{Δ S} & = 100 \times 25 \times 10^{- 4} \times \cos 0^{\circ} & = 0.25 {Nm}^{2} / C^{2} \end{aligned}$

So, the net flux through the cylinder,

$\begin{aligned} \oint ϕ & = \oint ϕ_{A} + \oint ϕ_{B} & = 0.125 + 0.25 & = 0.375 {Nm}^{2} / C^{2} \end{aligned}$

(ii) Using the Gauss’s law,

$\begin{aligned} ϕ & = \oint \vec{E} \cdot \vec{d s} = \frac{q}{ε_{0}} \Rightarrow 0.375 & = \frac{q}{8.85 \times 10^{- 12}} \Rightarrow q & = 8.85 \times 10^{- 12} \times 0.375 & = 3.3 \times 10^{- 12} C . & [C B S E Marking Scheme, 2013] \end{aligned}$

Electric Charges And Fields

electric-charges-and-fields Question 51

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Electric Charges And Fields

electric-charges-and-fields Question 51

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu