electric-charges-and-fields Question 45
Question: Q. 2. An electron falls through a distance of
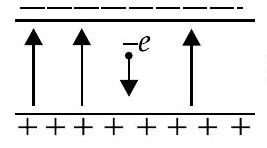
(a)
Calculate the time it takes to fall through this distance starting from rest.
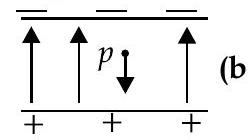
If the direction of the field is reversed (fig. b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest. A&E [OD Comptt. I, II, III 2018]
Show Answer
Solution:
Ans. Relevant formulae 1
Calculation of time taken by the electron Calculation of time taken by the proton We have
Force
Acceleration
Also
(i) For the electron
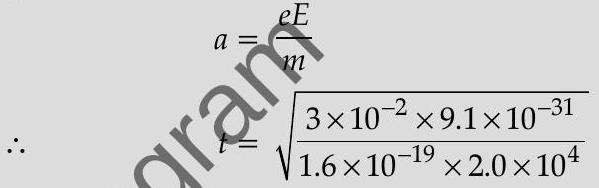
(ii) for proton






