Question: Q. 2. An electron falls through a distance of $1.5 \mathrm{~cm}$ in a uniform electric field of magnitude $2.0 \times 10^{4} \mathrm{~N} / \mathrm{C}$
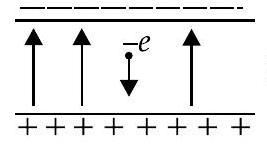
(a)
Calculate the time it takes to fall through this distance starting from rest.
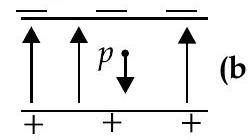
If the direction of the field is reversed (fig. b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest. A&E [OD Comptt. I, II, III 2018]
Show Answer
Solution:
Ans. Relevant formulae 1
Calculation of time taken by the electron Calculation of time taken by the proton We have
Force $=q \mathrm{E}$
Acceleration
$$ a=\frac{q E}{m} $$
Also
$$ \begin{aligned} & s=\frac{1}{2} a t^{2} \quad \text { as } u=0 \ & t=\sqrt{\frac{2 s}{a}} \end{aligned} $$
(i) For the electron
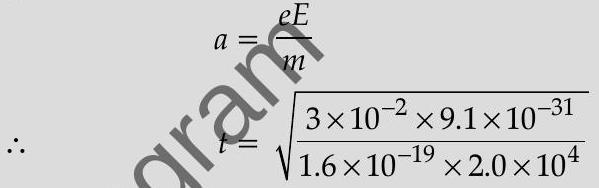
(ii) for proton
$$ =2.92 \mathrm{~ns} $$
$$ \begin{aligned} t & =\sqrt{\frac{2 \times 1.5 \times 10^{-2} \times 1.67 \times 10^{-27}}{1.6 \times 10^{-19} \times 2 \times 10^{4}}} \ = & 0.125 \mu \mathrm{s} \ & {[\text { CBSE Marking Scheme, } 2018] } \end{aligned} $$
