Solution:

Ans. Derivation of expression for electric field $\vec{E}_{e}$ due to dipole 3

Shape of the graph between $\left|E_{e}\right|$ and $r$ when $r»a$

Expression for torque acting on dipole

1

[CBSE Marking Scheme, 2014]

Detailed Answer :

Derivation of expression for electric field $\vec{E}_{e}$ due to dipole :

Try yourself, Similar to Q. 4 Long Answer Type. 1/2

Shape of the graphbetween $\left|E_{e}\right|$ and $r$ when $r»a$ :

Try yourself, Similar to Q. 1 (ii), Long Answer

Type Questions. $\quad 1 \frac{1}{2}$

Expression for torque acting on dipole : 2

Try Yourself, Similar to Q. 2, Short Answer Type Questions-II.

TOPIC-2

Gauss’s Theorem and Its Applications

Revision Notes

Electric Flux

Electric flux is proportional tolygraic number of electric field lines leaving the surface, outgoing lines with positive sign, incoming tines with negative sign.

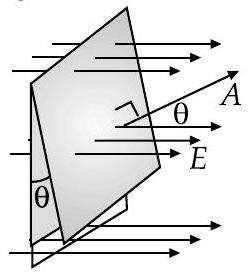
D Due to arbitrary arrangement of electric field lines, electric flux can be quantify as $\phi_{\mathrm{E}}=E A$

If vector $A$ is perpendicular to surface, magnitude of vector $A$ parallel to electric field is $A \cos \theta$

$A_{\text {II }}=A \cos \theta$

$\phi_{\mathrm{E}}=E A_{\mathrm{II}}=E A \cos \theta$

In non-uniform electric field, the flux will be $\phi_{E}=\int E d A$

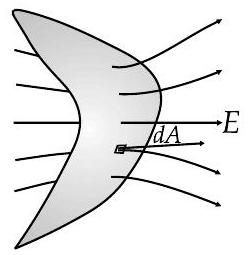
Continuous Charge Distribution

It is a system in which the charge is uniformly distributed over the material. In this system, infinite number of charges are closely packed and have minor space among them. Unlikely from the discrete charge system, the continuous charge distribution is uninterrupted and continuous in the material. There are three types of continuous charge distribution system.

For linear Charge Distribution $(\lambda), \vec{F}=\frac{q_{0}}{4 \pi \varepsilon_{0}} \int_{x} \frac{\lambda}{r^{2}} d X \hat{r}$

(Where, $\lambda=$ linear charge density)

For surface Charge Distribution $(\sigma), \vec{F}=\frac{q_{0}}{4 \pi \varepsilon_{0}} \int_{s} \frac{\sigma}{r^{2}} d \hat{r} \quad$ (Where, $\sigma=$ surface charge density)

For volume Charge Distribution (p), $\vec{F}=\frac{q_{0}}{4 \pi \varepsilon_{0}} \int_{v} \frac{\rho}{r^{2}} d V \hat{r} \quad$ (Where, $\rho=$ volume charge density)

Gauss law

• The net outward normal electric flux through any closed surface of any shape is equal to $1 / \varepsilon_{0}$ times to net charge enclosed by the surface :

The electric field flux at all points on Gaussian surface is $\phi=E \int d A=\frac{q}{\varepsilon_{0}}$

If there is a positive net flux, net positive charge is enclosed.

If there is a negative net flux, net negative charge is enclosed.

If there is zero net flux, no net charge is enclosed.

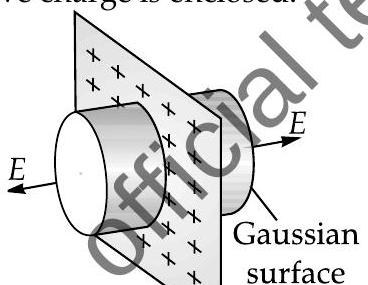
The equation for electric field due 10 point charge on Gaussian surface is $E=\frac{q}{4 \pi r^{2} \varepsilon_{0}}$

In an insulating sheet, chargeremains in the sheet, so electric field, $E=\frac{\sigma}{2 \varepsilon_{0}}$

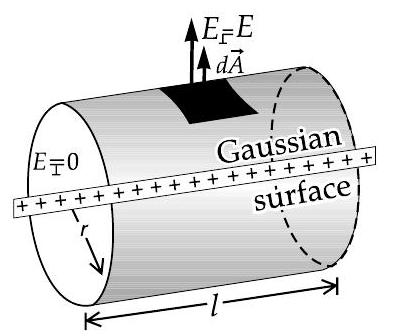
Gauss’ Law works in cases of cylindrical, spherical and rectangular symmetries.

The field outside the wire points radially outward which depends on distance from wire, $\vec{E}=\frac{\lambda}{2 \pi r \varepsilon_{0}} \hat{n}$, where, $\lambda$ is linear density of charge.

Closed surface : It is a surface which divides the space in inside and outside region, where one can’t move from one region to another without crossing the surface.

• Gaussian surface : It is a hypothetical closed surface having similar symmetry as problem on which we are working.

Electrostatic Shielding : It is the phenomenon of protecting certain region of space from external electric field.

Dielectric : The non-conducting material in which charges are easily produced on the application of electric field is called dielectric. e.g. Air, $\mathrm{H}_{2}$ gas, glass, mica, paraffin wax, transformer oil etc.

Key Formulae

$>$ Electric flux through an area $A$ :

• Electric flux through a Gaussian surface :

$$ \begin{aligned} \phi & =E . A=E A \cos \theta \ \phi & =\int E . d S \ \phi & =\frac{q_{e n c}}{\varepsilon_{0}} \end{aligned} $$

Gauss’s Law :

D Electric Field due to an infinite line of charge : $E=\frac{\lambda}{2 \pi \varepsilon_{0} r}=\frac{2 k \lambda}{r}$

where, $E=$ electric field $[\mathrm{N} / \mathrm{C}], \lambda=$ charge per unit length $[\mathrm{C} / \mathrm{m}]$

$\varepsilon_{0}=$ permittivity of free space $=8.85 \times 10^{-12}\left[\mathrm{C}^{2} / \mathrm{Nm}^{2}\right], r=$ distance $(\mathrm{m}), k=9 \times 10^{9} \mathrm{Nm}^{2} \mathrm{C}^{-2}$

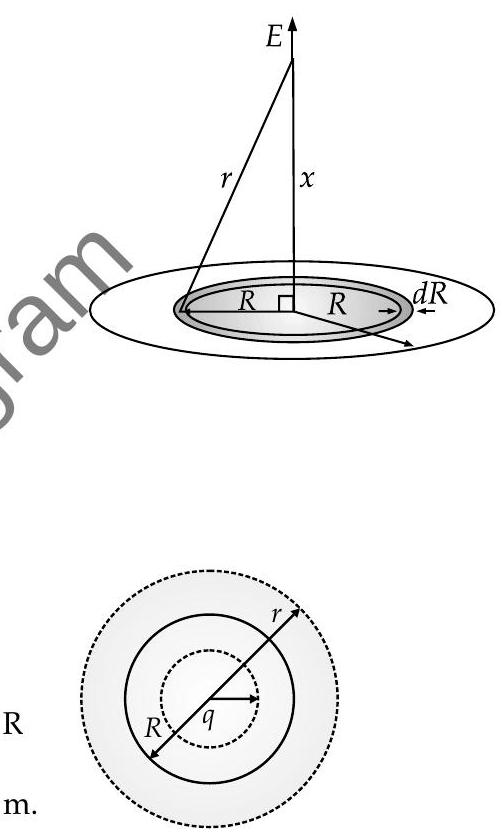
Electric field due to a ring at a distance $x$ is : $E=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q x}{\left(r^{2}+x^{2}\right)^{3 / 2}}$

When, $x»>\mathrm{r}$ :

When $x«<r$ :

Electric field due to a charged disc :

where,

$E=$ electric field $[\mathrm{N} / \mathrm{C}]$

$\varepsilon_{0}=8.85 \times 10^{-12}\left[\mathrm{C}^{2} / \mathrm{Nm}^{2}\right]$

$R=$ radius of the disc $[\mathrm{m}]$

Electric field due to a thin infinite sheet :

Electric field inside a spherical shell :

Electric field outside a spherical shell

$$ E=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{x^{2}} $$

$$ E=0 $$

$$ E=\frac{\sigma}{2 \varepsilon_{0}}\left[1-\frac{x}{\sqrt{R^{2}+x^{2}}}\right] $$

$\sigma=$ charge per unit area $\left[\mathrm{Cm}^{2}\right.$

$x=$ distance from charge $[\mathrm{m}]$

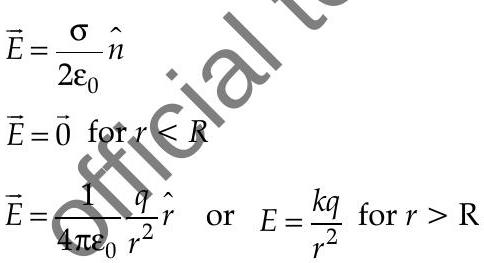
rell to the point of measurement in $\mathrm{m}$.

Objective Type Questions