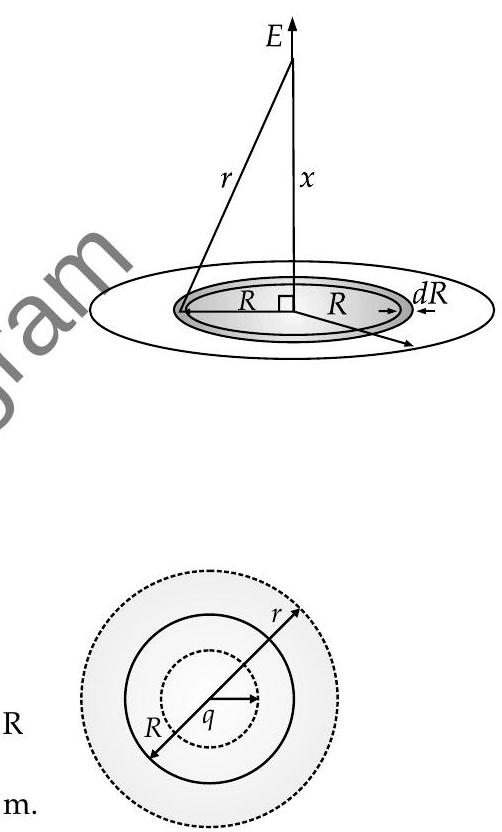
Question: Q. 5. A dipole is made up of two charges
R [O.D. I, II, III, 2014; CBSE SQP 2014]
Show Answer
Solution:
Ans. Derivation of expression for electric field
Shape of the graph between
Expression for torque acting on dipole
1
[CBSE Marking Scheme, 2014]
Detailed Answer :
Derivation of expression for electric field
Try yourself, Similar to Q. 4 Long Answer Type. 1/2
Shape of the graphbetween
Try yourself, Similar to Q. 1 (ii), Long Answer
Type Questions.
Expression for torque acting on dipole : 2
Try Yourself, Similar to Q. 2, Short Answer Type Questions-II.
TOPIC-2
Gauss’s Theorem and Its Applications
Revision Notes
Electric Flux
Electric flux is proportional tolygraic number of electric field lines leaving the surface, outgoing lines with positive sign, incoming tines with negative sign.
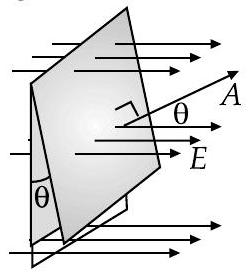
D Due to arbitrary arrangement of electric field lines, electric flux can be quantify as
If vector
In non-uniform electric field, the flux will be
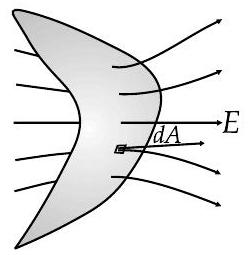
Continuous Charge Distribution
It is a system in which the charge is uniformly distributed over the material. In this system, infinite number of charges are closely packed and have minor space among them. Unlikely from the discrete charge system, the continuous charge distribution is uninterrupted and continuous in the material. There are three types of continuous charge distribution system.
For linear Charge Distribution
(Where,
For surface Charge Distribution
For volume Charge Distribution (p),
Gauss law
- The net outward normal electric flux through any closed surface of any shape is equal to
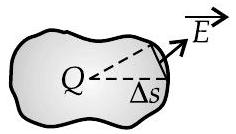
The electric field flux at all points on Gaussian surface is
If there is a positive net flux, net positive charge is enclosed.
If there is a negative net flux, net negative charge is enclosed.
If there is zero net flux, no net charge is enclosed.
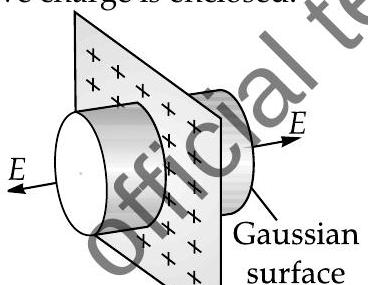
The equation for electric field due 10 point charge on Gaussian surface is
In an insulating sheet, chargeremains in the sheet, so electric field,
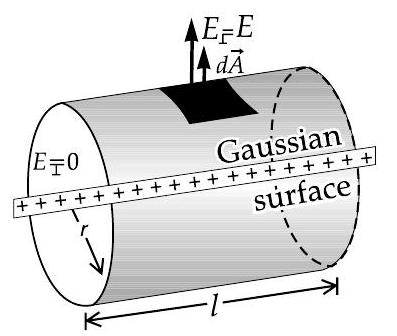
Gauss’ Law works in cases of cylindrical, spherical and rectangular symmetries.
The field outside the wire points radially outward which depends on distance from wire,
, where, is linear density of charge.
Closed surface : It is a surface which divides the space in inside and outside region, where one can’t move from one region to another without crossing the surface.
- Gaussian surface : It is a hypothetical closed surface having similar symmetry as problem on which we are working.
Electrostatic Shielding : It is the phenomenon of protecting certain region of space from external electric field.
Dielectric : The non-conducting material in which charges are easily produced on the application of electric field is called dielectric. e.g. Air,
Key Formulae
- Electric flux through a Gaussian surface :
Gauss’s Law :
D Electric Field due to an infinite line of charge :
where,
Electric field due to a ring at a distance
is :
When,
When
Electric field due to a charged disc :
where,
Electric field due to a thin infinite sheet :
Electric field inside a spherical shell :
Electric field outside a spherical shell
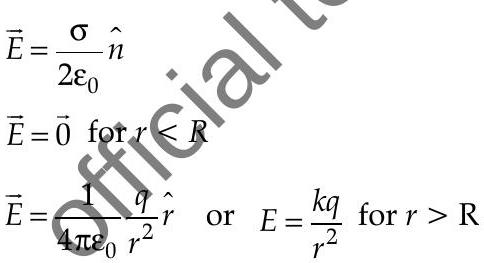
rell to the point of measurement in