electric-charges-and-fields Question 28
Question: Q. 12. (i) A point charge $(+Q)$ is kept in the vicinity of an uncharged conducting plate. Sketch electric field lines between the charge and the plate.
(ii) Two infinitely large plane thin parallel sheets having surface charge densities $\sigma_{1}$ and $\sigma_{2}$ $\left(\sigma_{1}>\sigma_{2}\right)$ are shown in the figure. Write the magnitudes and directions of the fields in the regions marked II and III.
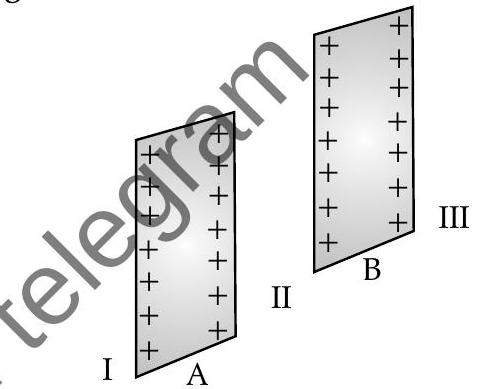
[Foreign Set I, II, III 2014]
Show Answer
Solution:
Ans. (i)
(ii) (a) For region II,
$$ E_{I I}=\frac{1}{2 \varepsilon_{0}}\left(\sigma_{1}-\sigma_{2}\right) $$
towards right side from sheet $\mathrm{A}$ to sheet $\mathrm{B}$. $1 / 2$
(b) For region III,
$$ E_{I I I}=\frac{1}{2 \varepsilon_{0}}\left(\sigma_{1}+\sigma_{2}\right) \quad 1 / 2 $$
towards right side away from the two sheets. $1 / 2$
[CBSE Marking Scheme, 2014]
Long Answer Type Questions
(5 marks each)
[AI Q. 1. (i) Derive an expression for electric field $E$ due to a dipole of length ’ $2 a$ ’ at a distant point ’ $r$ ’ from the centre of the dipole on an axial line.
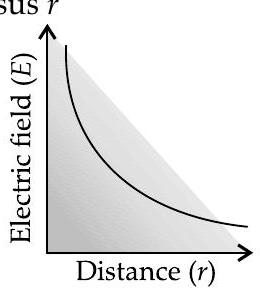
(ii) Draw a graph of $E$ versus $r$ for $r»a$
(iii) If this dipole were kept in a uniform external electric field $E_{0}$, diagrammatically represent the position of the dipole in stable and unstable equilibrium and write the expressions for the torque acting on the dipole in both the cases.
U [O.D. I, II, III 2017] Ans. (i) Derivation of $E$ along the axial line of dipole 2
(ii) Graph of $E$ versus $r$
(iii) (a) Diagrams for stable and unstable equilibrium of dipole
$1 / 2+1 / 2$
(b) Torque on dipole in both the cases $1 / 2+1 / 2$
[CBSE Marking Scheme, 2017]
Detailed Answer:
(i) Derivation of $E$ along the axial line of dipole Try yourself, Similar to Question 6, Short Answer Type Questions-I
(ii) Graph of $E$ versus $r$
(iii) (a) Diagrams for stable and unstable equilibrium of dipole.
Try yourself Similar to Question 1 (ii), Short Answer Type Questions-II
(b) Torque on dipole in both the cases.
Torque on dipole $=p E \sin \theta$
for stable equilibrium
$\theta=0^{\circ}$
$\therefore$ Torque $=0$
For unstable equilibrium
$\theta=180^{\circ}$
Then new Torque $=0$
