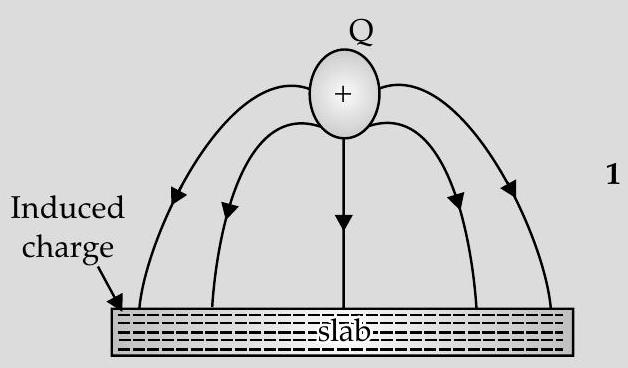
Question: Q. 12. (i) A point charge
(ii) Two infinitely large plane thin parallel sheets having surface charge densities
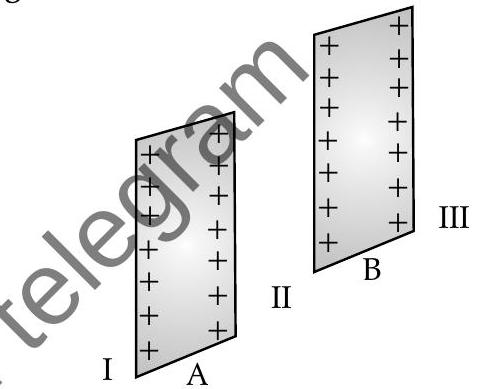
[Foreign Set I, II, III 2014]
Show Answer
Solution:
Ans. (i)
(ii) (a) For region II,
towards right side from sheet
(b) For region III,
towards right side away from the two sheets.
[CBSE Marking Scheme, 2014]
Long Answer Type Questions
(5 marks each)
[AI Q. 1. (i) Derive an expression for electric field
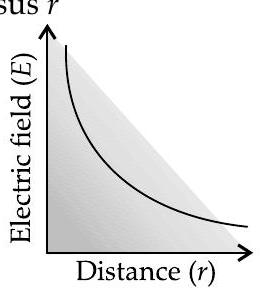
(ii) Draw a graph of
(iii) If this dipole were kept in a uniform external electric field
U [O.D. I, II, III 2017]
Ans. (i) Derivation of
(ii) Graph of
(iii) (a) Diagrams for stable and unstable equilibrium of dipole
(b) Torque on dipole in both the cases
[CBSE Marking Scheme, 2017]
Detailed Answer:
(i) Derivation of
(ii) Graph of
(iii) (a) Diagrams for stable and unstable equilibrium of dipole.
Try yourself Similar to Question 1 (ii), Short Answer Type Questions-II
(b) Torque on dipole in both the cases.
Torque on dipole
for stable equilibrium
For unstable equilibrium
Then new Torque






