electric-charges-and-fields Question 26
Question: Q. 10. An electric dipole is placed in a uniform electric field.
(i) Show that no translatory force acts on it.
(ii) Derive an expression for the torque acting on it.
(iii) Find work done in rotating the dipole through $180^{\circ}$.
A [Delhi Comptt. I, II, III, 2014,
O.D. I, II, III, 2013, 2012]
Show Answer
Solution:
Ans. Electric dipole of charges $+q$ and $-q$ separated by distance $2 a$ is shown in the figure.
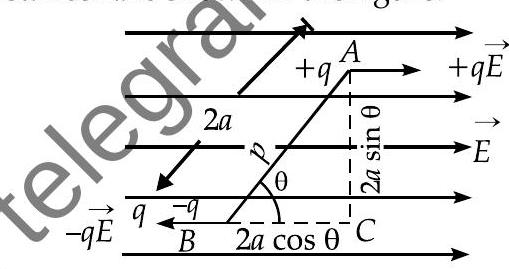
It is placed in a uniform electric field at an angle $\theta$ with it.
(i) Force on charge $+q, \overrightarrow{F_{1}}=q \vec{E}$, in the direction of $\vec{E}$.
$1 / 2$
Force on charge $-q, \overrightarrow{F_{2}}=-q \vec{E}$, in the opposite
direction of $\vec{E}$.
$\therefore$ Net translatory force on dipole $=\vec{F}{1}+\overrightarrow{F{2}}$
$$ =+q \vec{E}-q \vec{E}=\overrightarrow{0} $$
Hence, no translatory force acts on it.
$1 / 2$
(ii) But the two equal, parallel and unlike forces form a couple in which a torque is given by
$$ \begin{aligned} & \tau=\text { Force } \times \text { perpendicular distance } \ & \text { between the two forces } \end{aligned} $$
where, $\quad p=q \times 2 a=$ dipole moment
(iii) Work done in rotating the dipole through $180^{\circ}$ is
$$ \begin{aligned} & \mathrm{W}=\int d \mathrm{~W} \ & \mathrm{~W}=\int_{0^{\circ}}^{180^{\circ}} \tau d \theta=p \mathrm{E} \int_{0^{\circ}}^{180^{\circ}} \sin \theta d \theta \ & \mathrm{W}=p \mathrm{E}[-\cos \theta]_{0^{\circ}}^{180^{\circ}} \ & \mathrm{W}=-p \mathrm{E}\left[\cos 180^{\circ}-\cos 0^{\circ}\right] \ & \mathrm{W}=p \mathrm{E}[1+1]=2 p \mathrm{E} \end{aligned} $$
