Question: Q. 10. An electric dipole is placed in a uniform electric field.
(i) Show that no translatory force acts on it.
(ii) Derive an expression for the torque acting on it.
(iii) Find work done in rotating the dipole through
A [Delhi Comptt. I, II, III, 2014,
O.D. I, II, III, 2013, 2012]
Show Answer
Solution:
Ans. Electric dipole of charges
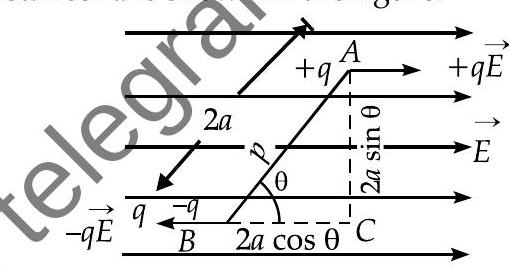
It is placed in a uniform electric field at an angle
(i) Force on charge
Force on charge
direction of
Hence, no translatory force acts on it.
(ii) But the two equal, parallel and unlike forces form a couple in which a torque is given by
where,
(iii) Work done in rotating the dipole through






