electric-charges-and-fields Question 16
Question: Q. 6. Find the expression for electric field intensity in an axial position due to electric dipole.
R [O.D. Comptt. I, II, III, 2013]
Show Answer
Solution:
Ans. Consider an electric dipole whose length is
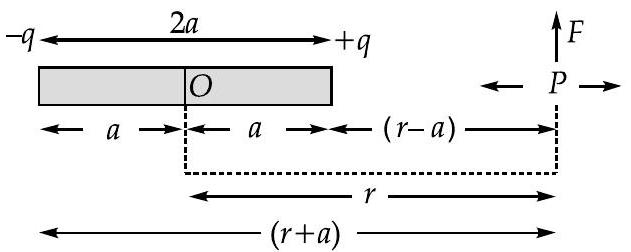
for,
Commonly Made Error
- Several candidates derivelan expression for intensity of electric field






