Question: Q. 2. Draw a graph showing the variation of de- Broglie wavelength $\lambda$ of a particle of charge $q$ and mass $m$, with the accelerating potential $V$. An $\alpha$-particle and a proton have the same de- Broglie wavelength equal to $1 \AA$. Explain with calculations, which of the two has more kinetic energy.

A [Delhi Comptt. II 2017]

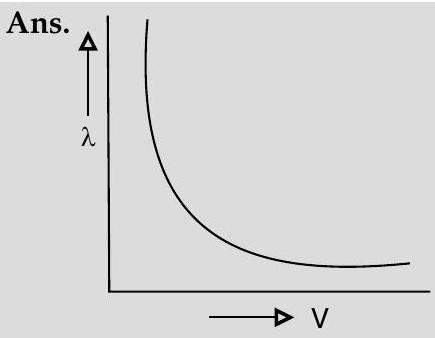
de-Broglie wavelength, $\lambda=\frac{h}{\sqrt{2 m q V}}$ and

$$ \text { K.E. }=K=q V $$

$$ \therefore \quad \lambda=\frac{h}{\sqrt{2 m K}} $$

Since, $\alpha$-particle and proton have same de-Broglie wavelength $1 \AA$

$$ \begin{array}{rlrl} & \therefore & \sqrt{2 m_{p}(K){p}} & =\sqrt{2 m{\alpha}(K){\alpha}} \ \Rightarrow & m{p}(K){p} & =m{\alpha}(K){\alpha} \ \text { as } & m{\alpha} & >m_{p} \ \Rightarrow & K . E_{p} & >\text { K.E. }_{\alpha} \end{array} $$

$\therefore$ Proton has more Kinetic energy.

Q.3. (i) Describe briefly how Davisson-Germer experiment demonstrated the wave nature of electrons.

(ii) An electron is accelerated from rest through a potential V. Obtain the expression for the de-Broglie wavelength associated with it. U] [Foreign 2014]

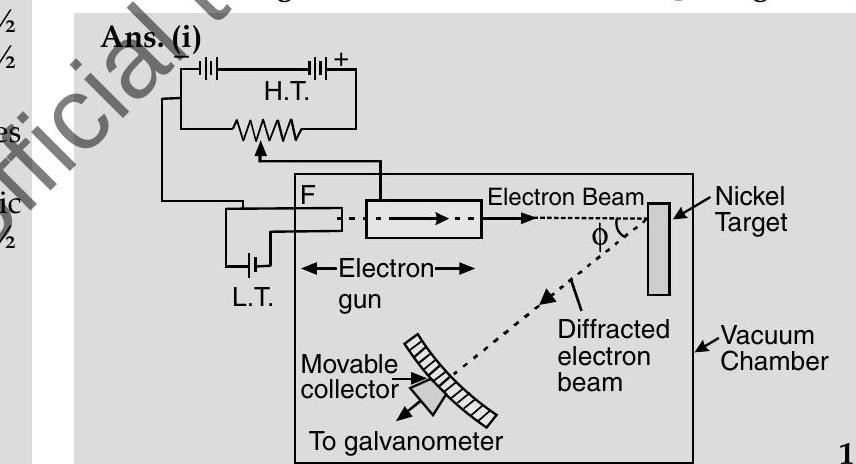
This experiment confirms the wave nature of electron.

$1 / 2$

(ii)

$$ \begin{aligned} & \lambda=\frac{h}{p}=\frac{h}{\sqrt{2 m K}} \ & \because \quad \mathrm{K}=\text { K.E. }=e V \ & \therefore \quad \lambda=\frac{h}{\sqrt{2 m e V}} \end{aligned} $$

[CBSE Marking Scheme 2014]

Detailed Answer :

(i) Davisson-Germer Experiment Setup :

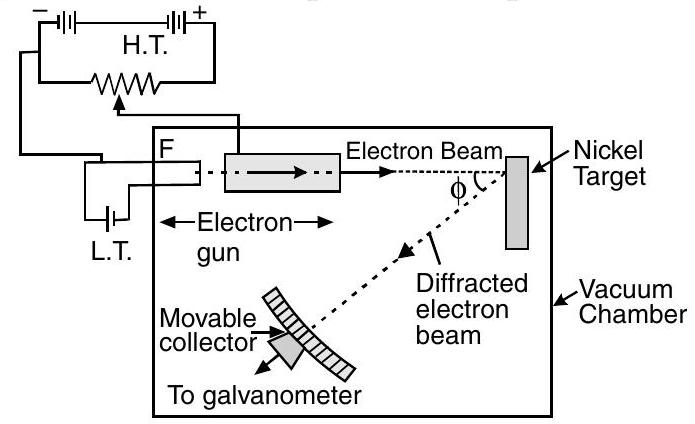(a) They used electron gun for firing electrons on Nickel metal.

(b) Electrons were accelerated to desired potential $V$.

(c) Interatomic space of Nickel acts as slit for diffracting electron waves.

(d) To avoid collisions of the electrons with other molecules on their way towards the surface, the experiment was conducted in a vacuum chamber.

(e) The intensity of scattered electrons was detected by electronic movable detector.

(f) The detector could move on a circular scale and was connected to a galvanometer.

(g) They plotted the radial graph with different scattered angles $V$ s. electron intensity (current) for different accelerating voltages from $44 \mathrm{~V}$ to $68 \mathrm{~V}$.

(h) Experimental reading showed a strong intensity peak $(I)$ of the scattered electron for an accelerating voltage of $54 \mathrm{~V}$ at a scattering angle $\phi=50^{\circ}$.

(i) By this they demonstrated the wave nature of electrons.

(ii) de-Broglie wavelength of matter

$$ \begin{equation*} \lambda=\frac{h}{p} \tag{i} \end{equation*} $$

Kinetic energy,

$$ \begin{aligned} K & =\frac{1}{2} m v^{2} \ K & =\frac{1}{2 m} m^{2} v^{2} \ K & =\frac{p^{2}}{2 m} \ p^{2} & =2 m K \ p & =\sqrt{2 m K} \end{aligned} $$

putting this expression of momentum $p$ in eq (1)

$$ \begin{equation*} \lambda= \tag{ii} \end{equation*} $$

If an electron accelerated with electric potential $V$; then its kinetic energy $\mathrm{K}=\mathrm{eV}$.

Putting this value of kinetic energy in eq. (ii)

$$ \lambda=\frac{h}{\sqrt{2 m e V}} $$

This is the desired expression.

Q. 4. The data given below gives the photon energy (in $\mathrm{eV}$ ) for a number of waves whose wavelength values (in $\mathrm{nm}$ ) are also given.

(Without doing any calculation/taking any reading), explain how one can use this data to draw an appropriate graph to infer

(i) photon energy corresponding to a wavelength of $100 \mathrm{~nm}$.

(ii) the wavelength value (in $\mathrm{nm}$ ) corresponding to a photon energy of $1 \mathrm{eV}$.

(iii) velocity of light, assuming that the value of Planck’s constant is known.

A [SQP 2014]