dual-nature-of-radiation-and-matter Question 19
Question: Q. 1. State Einstein’s photoelectric equation explaining the symbols used.
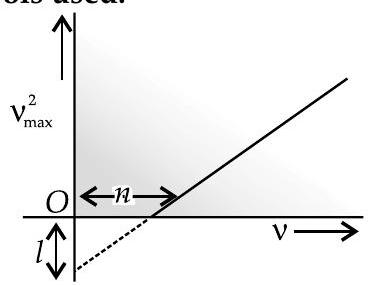
Light of frequency $v$ is incident on a photosensitive surface. A graph of the square of the maximum speed of the electrons $\left(v_{\text {max }}^{2}\right)$ vs. $v$ is obtained as shown in the figure. Using Einstein’s photoelectric equation, obtain expressions for (i) Planck’s constant. (ii) work function of the given photosensitive material in terms of parameters $l, n$ and mass of the electron $m$. [CBSE Comptt. 2018]
Show Answer
Solution:
Ans. Statement of equation with explanation of symbols
Expression for
(i) Planck’s constant
(ii) Work function
1
Einstein’s photoelectric equation is
$$ h v=W+\frac{1}{2} m v_{\max }^{2} $$
$v=$ frequency of incident light
$v_{0}=$ threshold frequency of photo sensitive material
$W=$ work function
$\frac{1}{2} m v_{\max }^{2}=$ max. kinetic energy of the emitted
photoelectrons $1 / 2$
(Also accept if the student writes
$$ h v=W+e V_{s} $$
$W=$ work function of photosensitive material
$V_{s}=$ Stopping Potential)
From Einstein’s photoelectric equation, we have
$$ \begin{aligned} h v & =W+\frac{1}{2} m v_{\text {max }}^{2} \ \therefore \quad v^{2}{ }_{\text {max }} & =\frac{2}{m}(h v-W) \ & =\left(\frac{2 h}{m}\right) v+\left(\frac{-2 W}{m}\right) \end{aligned} $$
Slope of the given graph $=\frac{T}{n}$
intercept on the $y$-axis $=-l$
$\therefore \quad \frac{2 h}{m}=\frac{l}{n}$ or $h=\frac{m l}{2 n}$
and
$$ -l=\frac{-2 W}{m} \text { or } W=\frac{m l}{2} $$
[CBSE Marking Scheme 2018]






