current-electricity Question 42
Question: Q. 4. A uniform wire of resistance
A [O.D. Comptt. I, II, III 2013]
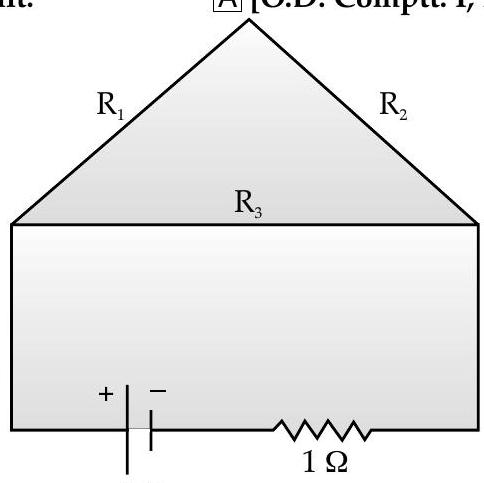
Show Answer
Solution:
Ans.
Let,
Total resistance
According to circuit :
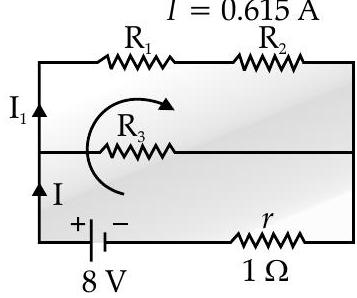
Let current across
and current across
So current across
Apply Kirchhoff’s
[AT Q. 5. The network
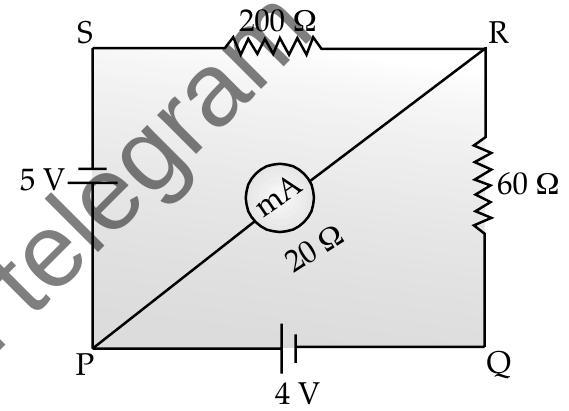
A [O.D. Comptt. I, II, III 2012]
Ans. Let us redraw circuit as shown.
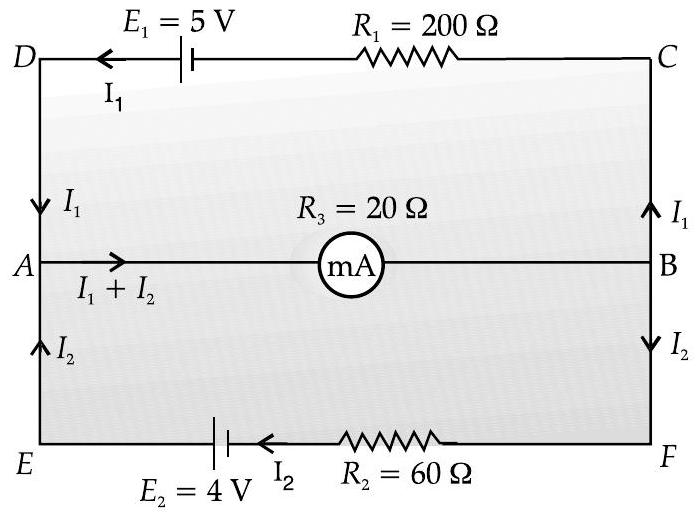
Using Kirchhoff’s voltage law in closed loop
In a closed loop
Substituting the values of
We have
Solving above equations, we get
Now, current in milliammeter






