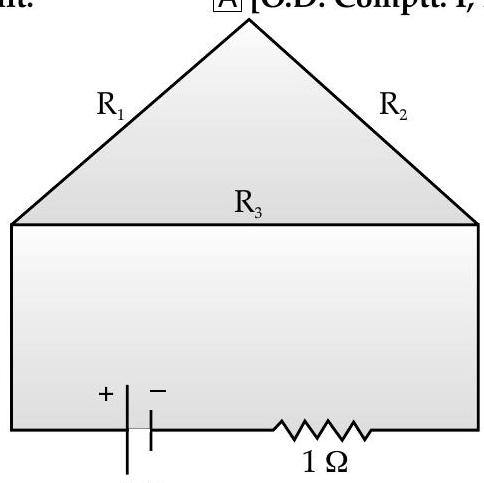
SATHEE: current-electricity Question 42

विद्युत् धारा

Question: Q. 4. A uniform wire of resistance $48 Ω$ is cut into three pieces so that the ratio of the resistances $R_{1} : R_{2}$ : $R_{3} = 1 : 2 : 3$ and the three pieces are connected to form a triangle across which a cell of emf $8 V$ and internal resistance $1 Ω$ is connected as shown. Calculate the current through each part of the circuit.

A [O.D. Comptt. I, II, III 2013]

$8 V$

Show Answer

Solution:

Ans.

$R_{1} : R_{2} : R_{3} = 1 : 2 : 3$

Let,

$\begin{aligned} R_{1} = R & R_{2} = 2 R & R_{3} = 3 R \end{aligned}$

Total resistance $(R_{T}) = R + 2 R + 3 R$

$\begin{array}{llrl} = 48 Ω ∴ & R & = 8 Ω Hence & R_{1} & = 8 Ω & R_{2} & = 16 Ω and & R_{3} & = 24 Ω \end{array}$

According to circuit :

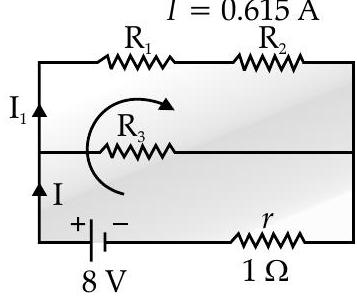
$\begin{aligned} E = I (R_{T} + r) & 8 = I (R_{T} + r) & 8 = I (12 + 1) & I = \frac{8}{13} A & I = 0.615 A & 8 \end{aligned}$

Let current across $R_{1}$ is $I_{1}$

and current across $R_{2}$ is $I_{2}$

So current across

$I_{2} = I_{1}$

$R_{3} = I_{3} = (I - I_{1})$

Apply Kirchhoff’s $2^{nd}$ Law

$\begin{aligned} I_{1} & = \frac{R_{3}}{(R_{1} + R_{2} + R_{3})} \times I & = \frac{24}{(8 + 16 + 24)} \times 0.615 1 / 2 I_{2} & = I_{1} = 0.3075 A I_{3} & = I - I_{1} & = 0.615 - 0.3075 & = 0.3075 A \end{aligned}$

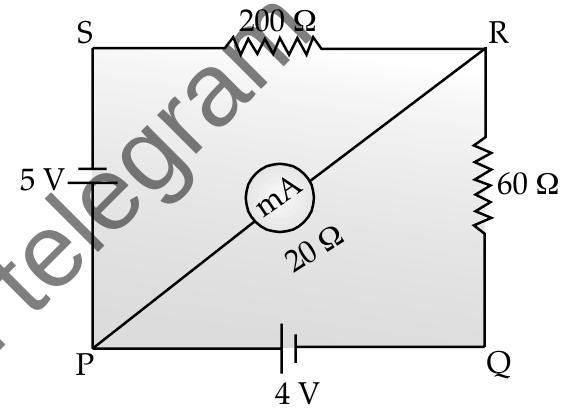
[AT Q. 5. The network $P Q R S$ , shown in the circuit diagram, has the batteries of $4 V$ and $5 V$ and negligible internal resistance. A milliammeter of $20 Ω$ resistance is connected between $P$ and $R$ . Calculate the reading in the milliammeter.

A [O.D. Comptt. I, II, III 2012]

Ans. Let us redraw circuit as shown.

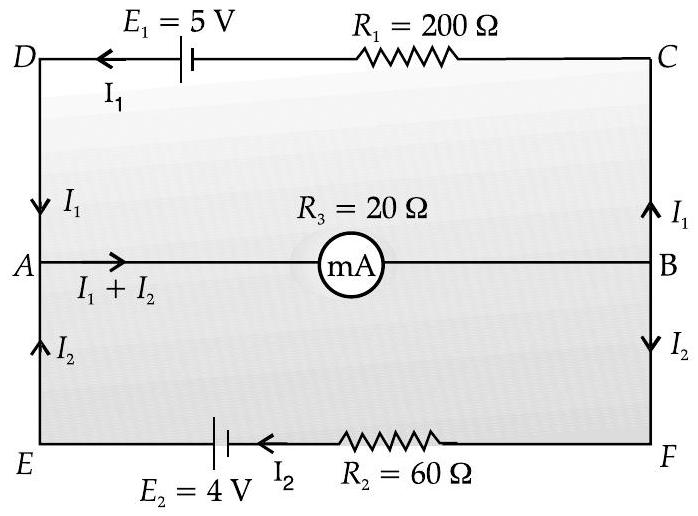
Using Kirchhoff’s voltage law in closed loop $D A B C D$

$\begin{matrix} (i) & (I_{1} + I_{2}) R_{3} + I_{1} R_{1} - E_{1} = 0 \end{matrix}$

In a closed loop $A B F E A$

$\begin{matrix} (ii) & (I_{1} + I_{2}) R_{3} + I_{2} R_{2} - E_{2} = 0 \end{matrix}$

Substituting the values of $Misplaced &$ in equations (i) & (ii)

We have $44 I_{1} + 4 I_{2} = 1$

$and 5 I_{1} + 20 I_{2} = 1$

Solving above equations, we get

$Misplaced &$

Now, current in milliammeter

$\begin{aligned} I_{m} & = I_{1} + I_{2} & = 0 \cdot 0186 A + 0 \cdot 0454 A & = 0 \cdot 064 A = 64 mA \end{aligned}$

विद्युत् धारा

विषयसूची

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

विद्युत् धारा

विषयसूची

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu