Solution:

Ans. (i) $V=\mathrm{Ir}$ (without voltmeter)

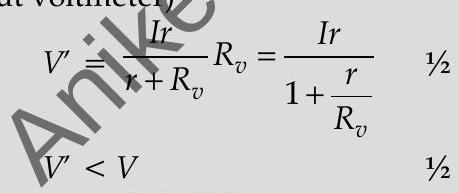
(ii) Percentage error $=\left(\frac{V-V^{\prime }}{V}\right)\times 1001/2$

$$=\left(\frac{r}{r+R_v}\right)\times 100$$

(iii) $R_v\to \mathrm{\infty },V^{\prime }=Ir=V$

[CBSE Marking Scheme, 2016]

[I] Q. 17. In the two electric circuits shown in the figure, determine the readings of ideal ammeter $(A)$ and the ideal voltmeter $(V)$.

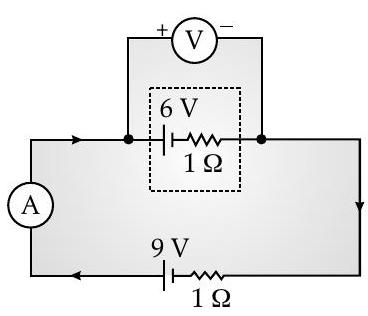
(b)

A [Delhi I, II, III 2015]

Ans. In circuit (a),

(a)

Total Resistance $=2\mathrm{\Omega }$

$$\text{ Current }i=(15/2)\mathrm{A}=7.5\mathrm{A}1/2$$

Potential difference between the terminals of $6\mathrm{V}$ battery

In circuit (b),

$$\begin{array}{rlrl}V& =E-ir& =[6-(7.5\times 1)]\mathrm{V}V& =-1.5\mathrm{V}\end{array}$$

$$\begin{array}{rlr}\text{ Effective emf }& =(9-6)\mathrm{V}& =3\mathrm{V}\end{array}$$

Total resistance $=2\mathrm{\Omega }$

Current,

$$i=\left(\frac{3}{2}\right)\mathrm{A}=1.5\mathrm{A}$$

Potential difference across $6\mathrm{V}$ cell

$$\begin{array}{rlrl}V& =E+ir& =6+1.5\times 1& =7.5\mathrm{V}\end{array}$$

(AI Q. 1. (i) Derive an expression for drift velocity of electrons in a conductor. Hence deduce Ohm’s law.

(ii) A wire whose cross-sectional area is increasing linearly from its one end to the other, is connected across a battery of $\mathrm{V}$ volts. Which of the following quantities remain constant in the wire?

(a) drift speed

(b) current density (c) electric current

(d) electric field

Justify your answer.

A [Delhi I, II, III 2017]

Ans. (i) Derivation of the expression for drift velocity 2

Deduction of Ohm’s law

2

(ii) Name of quantity and justification $1/2+1/2$

(i) Let an electric field $E$ be applied to the conductor. Acceleration of each electron is

$$a=-\frac{eE}{m}$$

Velocity gained by the electron

$$v=-\frac{eE}{m}t$$

Let the conductor contain $n$ electrons per unit volume. The average value of time ’ $t$ ‘, between their successive collisions, is the relaxation time, ’ $\tau$ ‘.

Hence average drift velocity, $v_d=\frac{-eE}{m}\tau$

The amount of charge, crossing area $A$, in time $\mathrm{\Delta }t$, is $=neA{v}_d\mathrm{\Delta }t=I\mathrm{\Delta }t$

Substituting the value of $v_d$, we get

$$\begin{array}{rlrlr}I\mathrm{\Delta }t& =neA\left(\frac{eE\tau }{m}\right)\mathrm{\Delta }t\therefore I& =\left(\frac{e^{2}A\tau n}{m}\right)E\therefore \frac{I}{A}& =\left(\frac{e^2\tau n}{m}\right)E& =\sigma E(\sigma =\frac{e^2\tau n}{m}\text{ is the conductivity })\end{array}$$

But $I=JA$, where, $J$ is the current density,

$\Rightarrow \mathrm{J}=\left(\frac{e^2\tau n}{m}\right)E$

$\Rightarrow \mathrm{J}=\sigma E$

This is Ohm’s law

[Note : Credit should be given if the student derives the alternative form of Ohm’s law by substituting $E=\frac{V}{l}$ ]

(ii) (b) Current density will remain constant in the wire.

All other quantities, depend on the cross sectiona area of the wire.

[CBSE Marking Scheme 2017]

Detailed Answer :

(ii) Out of these, current density remains constant in a wire whose cross-sectional area increases linearly from its one end to other as current density is :

$$\begin{array}{rlr}J& =\frac{I}{A}\text{ and }I=\frac{V}{R}\therefore & J=\frac{V}{RA}\text{ and }R=\rho \frac{l}{A}\end{array}$$

$$\therefore =\frac{VA}{\rho lA}=\frac{V}{\rho l}=\text{ constant }$$

It is current per unit area that depends on area of cross-section.

$1/2$

Drift speed is given as :

$$v_d=\frac{I}{\text{ Ane }}$$

Electric field $=\frac{J}{\sigma }$; where $\sigma$ is electrical conductivity

$1/2$