Question: Q. 16. The potential difference across a resistor ’
(i) Now if the potential difference across ’
(ii) Find the percentage error in measuring the potential difference by a voltmeter.
(iii) At what value of
U] [CBSESQP 2015-16]
Show Answer
Solution:
Ans. (i)
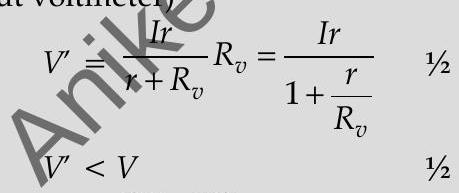
(ii) Percentage error
(iii)
[CBSE Marking Scheme, 2016]
[I] Q. 17. In the two electric circuits shown in the figure, determine the readings of ideal ammeter
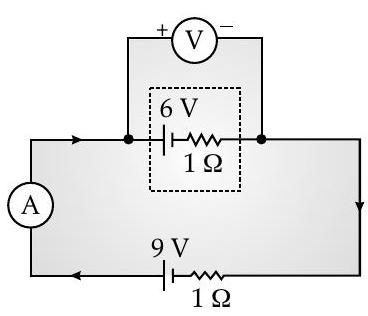
(b)
A [Delhi I, II, III 2015]
Ans. In circuit (a),
(a)
Total Resistance
Potential difference between the terminals of
In circuit (b),
Total resistance
Current,
Potential difference across
(AI Q. 1. (i) Derive an expression for drift velocity of electrons in a conductor. Hence deduce Ohm’s law.
(ii) A wire whose cross-sectional area is increasing linearly from its one end to the other, is connected across a battery of
(a) drift speed
(b) current density (c) electric current
(d) electric field
Justify your answer.
A [Delhi I, II, III 2017]
Ans. (i) Derivation of the expression for drift velocity 2
Deduction of Ohm’s law
2
(ii) Name of quantity and justification
(i) Let an electric field
Velocity gained by the electron
Let the conductor contain
Hence average drift velocity,
The amount of charge, crossing area
Substituting the value of
But
This is Ohm’s law
[Note : Credit should be given if the student derives the alternative form of Ohm’s law by substituting
(ii) (b) Current density will remain constant in the wire.
All other quantities, depend on the cross sectiona area of the wire.
[CBSE Marking Scheme 2017]
Detailed Answer :
(ii) Out of these, current density remains constant in a wire whose cross-sectional area increases linearly from its one end to other as current density is :
It is current per unit area that depends on area of cross-section.
Drift speed is given as :
Electric field






