current-electricity Question 31
Question: Q. 6. (i) The potential difference applied across a given resistor is altered so that the heat produced per second increases by a factor of 9 . By what factor does the applied potential difference change?
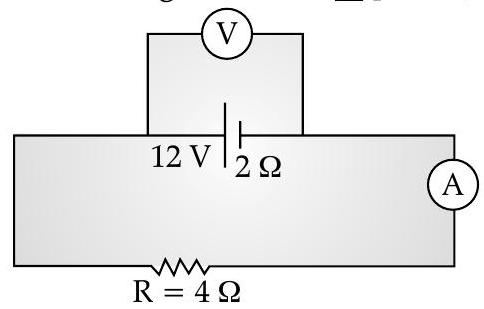
(ii) In the figure shown, an ammeter $A$ and a resistor of $4 \Omega$ are connected to the terminals of the source. The emf of the source is $12 \mathrm{~V}$ having an internal resistance of $2 \Omega$. Calculate the voltmeter and ammeter readings.
R [O.D. I, II, III 2017]
Show Answer
Solution:
Ans. (i) The factor by which the potential difference changes
(ii) Ammeter Reading 1
(iii) Voltmeter Reading
$$ \begin{equation*} H=\frac{V^{2}}{R} \tag{i} \end{equation*} $$
$\therefore V$ increases by a factor of $\sqrt{9}=3$ (ii) Ammeter Reading, $I=\frac{V}{R+r}$
$$ =\frac{12}{4+2} \mathrm{~A}=2 \mathrm{~A} $$
(iii) Voltmeter Reading, $V=E-I r$
$$ =[12-(2 \times 2)] \mathrm{V}=8 \mathrm{~V} \quad 1 / 2 $$
(Alternatively, $V=i R=2 \times 4 \mathrm{~V}=8 \mathrm{~V}$ )
[CBSE Marking Scheme 2017]
Detailed Answer :
(i) Let the original potential difference be V volts with heat generated as $H$.
Now heat generated will be :
$$ \begin{equation*} H=\frac{V^{2} t}{R} \tag{1} \end{equation*} $$
Take the new potential difference as $V^{\prime}$ and change in heat produced be $H$ so,
Change in heat produced :
$$ \begin{equation*} H^{\prime}=\frac{V^{\prime 2} t}{R} \tag{2} \end{equation*} $$
But from the question, if the heat produced by a factor of 9 , so
$$ \begin{aligned} H^{\prime} & =9 H \ \frac{V^{\prime 2} t}{R} & =9 \times \frac{V^{2} t}{R} \ V^{\prime 2} & =9 V^{2} \ V^{\prime} & =3 V \end{aligned} $$
Hence, it is clear that the applied potential difference increases by factor 3 .
[AI Q. 7. Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
R [O.D. I, II, III 2012]
Ans. Relaxation time $(\tau)$ : The average time interval between two successive collisions for the free electrons drifting within a conductor (due to the action of the applied electric field), is called relaxation time.
Relation
1
$\begin{array}{rlrl} & & v_{d} & =(-e E \tau) / m \ & \text { Since } & i & =-n e A v_{d} \ & & & n e^{2} A \tau \mathrm{V} / m l \ & \therefore & V / i & =m l /\left(n e^{2} A \tau\right)=\rho l / A \ \therefore & \rho & =m /\left(n e^{2} \tau\right)\end{array}$
$1 / 2$
[CBSE Marking Scheme, 2012]
