SATHEE: alternating-currents Question 39

alternating-currents Question 39

Question: Q. 5. (i) Draw a labelled diagram of $a c$ generator. Derive the expression for the instantaneous value of the emf induced in the coil.

(ii) A circular coil of cross-sectional area $200 {cm}^{2}$ and 20 turns is rotated about the vertical diameter with angular speed of $50 rad s^{- 1}$ in a uniform magnetic field of magnitude $3.0 \times 10^{- 2} T$ . Calculate the maximum value of the current in the coil.

U] [Delhi I, II, III 2017]

Show Answer

Solution:

Ans. (i) Labelled diagram of $a c$ generator $11 / 2$ Expression for instantaneous value of induced emf.

(ii) Calculation of maximum value of current

(i) Labelled diagram :

Try yourself, Similar to Q. 3(a), Long Answer Type Questions

(ii) Maximum value of emf

$\begin{aligned} e_{0} = & NBA ω = & 20 \times 200 \times 10^{- 4} & \times 3 \times 10^{- 2} \times 50 V / \frac{1}{2} = & 600 mV \end{aligned}$

Maximum induced current,

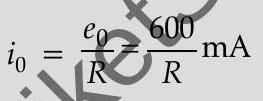
[Note 1 : If the student calculates the value of the maximum induced emf and says that “since $R$ is not given, the value of maximum induced current cannot be calculated”, the $1 / 2$ mark, for the last part, of the question, can be given.]

[Note 2 : The direction of magnetic field has not been given. If the student takes this direction along the axis of rotation and hence obtains the value of induced emf and, therefore, maximum current, as zero, award full marks for this part.]

[CBSE Marking Scheme 2017]

Detailed Answer :

(i) Expression :

If at any moment, $t$ be the perpendicular vector to the plane of coil that makes an angle $θ$ with direction of magnetic field $(B)$ , so flux passing through the coil will be :

$\begin{aligned} ϕ = n B A \cos θ & θ = ω t \end{aligned}$

$[ω =$ angular velocity of the coil] Now,

$\begin{matrix} (1) & ϕ = n A B \cos ω t \end{matrix}$

If $e$ is instantaneous induced emf produced in the coil, then

$\begin{aligned} e & = - \frac{d ϕ}{d t} & = - \frac{d (n A B \cos ω t)}{d t} & = - n A B ω (- \sin ω t) \end{aligned}$

Maximum value or peak value of instantaneous induced emf $e$ which is attained when $\sin ω t = \pm 1$

$∴ e_{max} = n ω A B$

So, $e = e_{max} \sin ω t$

As value of sine function varies from +1 to -1 , polarity of emf changes with time. Also the output voltage is sinusoidalin nature.

Alternating Currents

alternating-currents Question 39

Detailed Answer :

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Alternating Currents

alternating-currents Question 39

Detailed Answer :

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu