alternating-currents Question 29
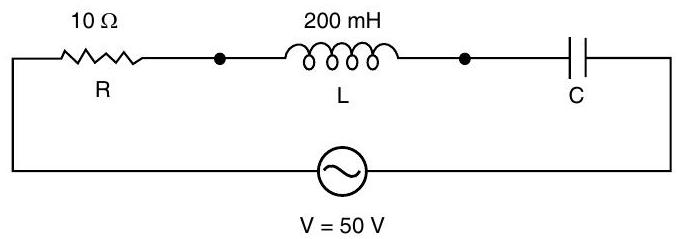
Question: Q. 4. In the following circuit, calculate (i) the capacitance of the capacitor, if the power factor of the circuit is unity, (ii) the Q-factor of this circuit. What is the significance of the Q-factor in ac circuit? Given the angular frequency of the
A [O.D. Comptt I, II, III 2017]
Show Answer
Solution:
Ans. (i) Calculation of Capacitance
(ii)
(i) As power factor is unity,
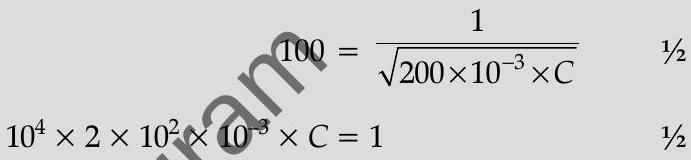
(ii) Quality factor,
Significance : It measures the sharpness of resonance.
Average Power dissipated,
[CBSE Marking Scheme 2017]
[A] Q. 5. An
A [SQP I 2017]
Ans. (i) Expression for Current and Phase angle 4
(ii) Resonance Frequency
1
(i) In a series
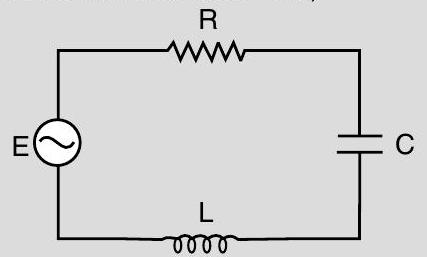
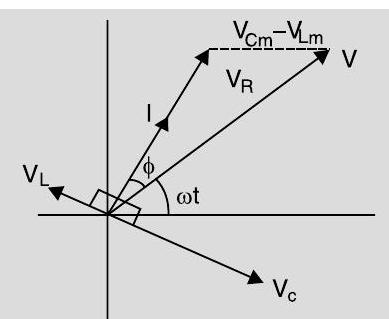
From the phasor relation, voltages
$$ \begin{aligned} & V_{m}^{2}=V_{R}^{2}+\left(V_{C m}-V_{L m}\right)^{2} \ & V_{m}^{2}=\left(\mathrm{I}{\mathrm{m}} R\right)^{2}+\left(\mathrm{I}{\mathrm{m}} X_{C}-\mathrm{I}{\mathrm{m}} X{L}\right)^{2} \ & V_{m}^{2}=\mathrm{I}{\mathrm{m}}{ }^{2}\left(R^{2}+\left(X{C}-X_{L}\right)^{2}\right) \end{aligned} $$
Now current in the circuit :
As phasor
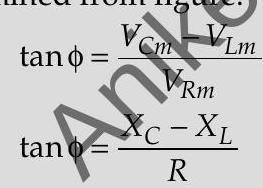
(ii) Resonance Frequency
Frequencies at which the response amplitude is relative maximum are known as system’s resonant frequencies. It is shown as :
[CBSE Marking Scheme 2017]






