alternating-currents Question 23
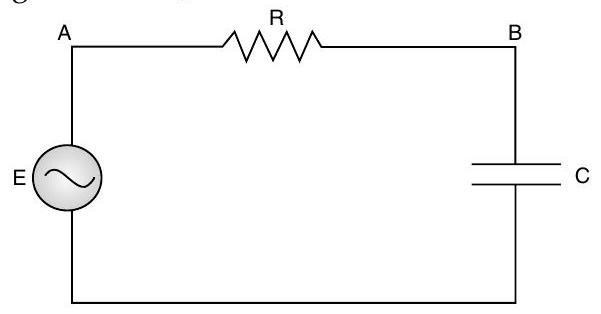
Question: Q. 11. A source of $a c$ voltage $\mathrm{V}=\mathrm{V}_{0} \sin \omega t$ is connected to a series combination of a resistor ’ $R$ ’ and a capacitor ’ $C$ ‘. Draw the phasor diagram and use it to obtain the expression for (i) impedance of the circuit and (ii) phase angle. U] [O.D. I, II, III 2015]
Show Answer
Solution:
Ans. The Pythagoras theorem gives
$$ V_{m}^{2}=V_{r m}^{2}+V_{c m}^{2} $$
Substituting the values of $V_{r m}$ and $V_{c m}$ into this equation, gives
$$ \begin{aligned} V_{m}^{2} & =\left(i_{m} R\right)^{2}+\left(i_{m} X_{C}\right)^{2} \ & =i_{m}^{2}\left(R^{2}+X_{C}^{2}\right) \ i_{m} & =\frac{V_{m}}{\sqrt{R^{2}+X_{C}^{2}}} \end{aligned} $$
$\therefore$ The impedance of the circuit is given by :
$$ Z=\sqrt{R^{2}+X_{C}^{2}}=\sqrt{R^{2}+\frac{1}{\omega^{2} C^{2}}} $$
The phase angle is the angle between $V_{\mathrm{R}}$ and $V$. Hence
$$ \tan \phi=\frac{X_{C}}{R}=\frac{1}{\omega C R} $$
$1 / 2$
The circuit diagram and the phasor diagram, for the given circuit, are as shown.
