Work Energy and Power - Result Question 5
7. A vertical spring with force constant $k$ is fixed on a table. A ball of mass $m$ at a height $h$ above the free upper end of the spring falls vertically on the spring so that the spring is compressed by a distance $d$. The net work done in the process is
[2007]
(a) $m g(h+d)-\frac{1}{2} k d^{2}$
(b) $m g(h-d)-\frac{1}{2} k d^{2}$
(c) $mg(h-d)+\frac{1}{2} kd^{2}$
(d) $mg(h+d)+\frac{1}{2} kd^{2}$
Show Answer
Answer:
Correct Answer: 7. (a)
Solution:
$ =8+5 $
$ =13 J . $
. (a)
$W=$ Potential energy stored in the spring + Loss of potential energy of mass
$\Rightarrow W_a=-8.75 J$
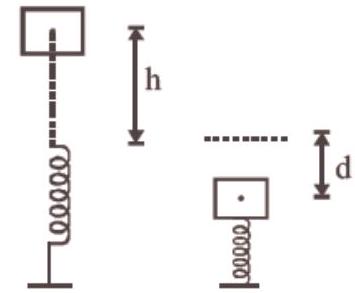
which is the work done due to air resistance
Work done due to gravity $=mgh$
$=10^{-3} \times 10 \times 10^{3}=10 J$
$W=m g(h+d)-\frac{1}{2} k d^{2}$
Gravitational potential energy of ball gets converted into elastic potential energy of the spring.
$m g(h+d)=\frac{1}{2} k d^{2}$
Net work done $=mg(h+d)-\frac{1}{2} k d^{2}=0$
$\frac{W_P}{W_Q}=\frac{\frac{1}{2} k_p x^{2}}{\frac{1}{2} k_Q x^{2}}=\frac{k_p}{k_Q}$
As $k_p>k_Q$ so, $W_p>W_Q$
