System of Particles and Rotational Motion - Result Question 46
49. A weightless ladder $20 ft$ long rests against a frictionless wall at an angle of $60^{\circ}$ from the horizontal. A 150 pound man is $4 ft$ from the top of the ladder. A horizontal force is needed to keep it from slipping. Choose the correct magnitude of the force from the following
(a) $175 lb$
(b) $100 lb$
(c) $120 lb$
(d) $69.2 lb$
[1998]
Show Answer
Answer:
Correct Answer: 49. (d)
Solution:
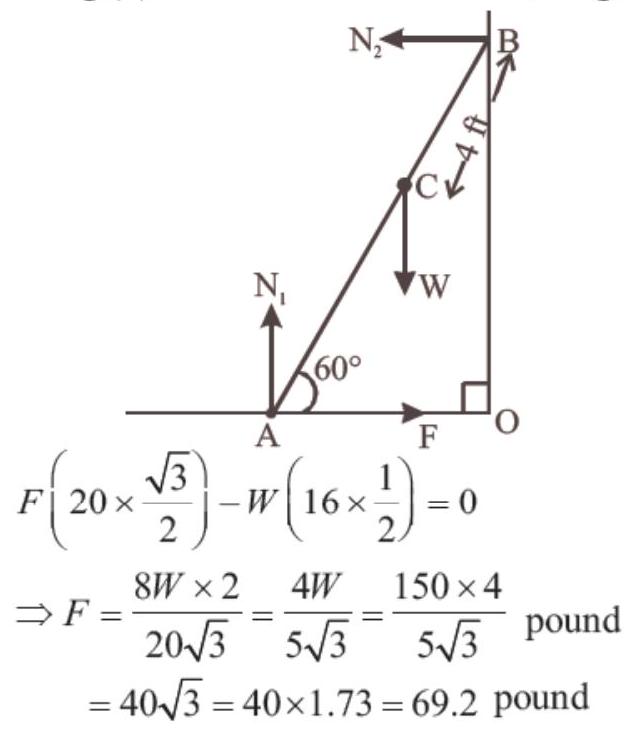
- (d) $A B$ is the ladder, let $F$ be the horizontal force and $W$ is the weight of man. Let $N_1$ and $N_2$ be normal reactions of ground and wall, respectively. Then for vertical equilibrium $W=N_1$
For horizontal equilibrium, $N_2=F$
Taking moments about $A$, $N_2(A B \sin 60^{\circ})-W(A C \cos 60^{\circ})=0$
Using (2) and $A B=20 ft, B C=4 ft$, we get
