Ray Optics and Optical Instruments - Result Question 65
68. A astronomical telescope has objective and eyepiece of focal lengths $40 cm$ and $4 cm$ respectively. To view an object $200 cm$ away from the objective, the lenses must be separated by a distance :
(a) $37.3 cm$
(b) $46.0 cm$
(c) $50.0 cm$
(d) $54.0 cm$
[2016]
Show Answer
Answer:
Correct Answer: 68. (d)
Solution:
- (d) Given: Focal length of objective, $f_0=40 cm$ Focal length of eye - piece $f_e=4 cm$ image distance, $v_0=200 cm$
Using lens formula for objective lens
$\frac{1}{v_0}-\frac{1}{u_0}=\frac{1}{f_0} \Rightarrow \frac{1}{v_0}=\frac{1}{f_0}+\frac{1}{u_0}$
$\Rightarrow \frac{1}{v_0}=\frac{1}{40}+\frac{1}{-200}=\frac{+5-1}{200}$
$\Rightarrow v_0=50 cm$
Tube length $\ell=|v_0|+f_e=50+4=54 cm$.
In a telescope, if field and eye lenses are interchanged magnification will change from $(\frac{f_o}{f_e})$ to $(\frac{f_e}{f_o})$ i.e., it will change from $m$ to $\frac{1}{m}$ i.e., will become $(\frac{1}{m^{2}})$ times of its initial value.
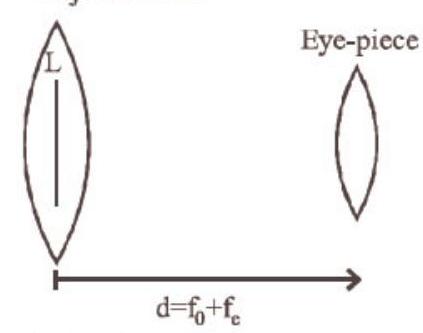
Magnification by eye piece
$ \begin{aligned} & m=\frac{f}{f+u} \\ & -\frac{I}{L}=\frac{f_e}{f_e+[-(f_0+f_e)]}=-\frac{f_e}{f_0} \text{ or, } \frac{I}{L}=\frac{f_e}{f_0} \\ & \text{ Magnification, } M=\frac{f_0}{f_e}=\frac{L}{I} \end{aligned} $






