Ray Optics and Optical Instruments - Result Question 38
38. A convex lens and a concave lens, each having same focal length of $25 cm$, are put in contact to form a combination of lenses. The power in diopters of the combination is
(a) 50
(b) infinite
(c) zero
(d) 25
[2006]
Show Answer
Answer:
Correct Answer: 38. (c)
Solution:
- (c) From the formula,
$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}=\frac{1}{25}-\frac{1}{25}=0$
Power of combination $=\frac{1}{f}=0$
39
$\frac{1}{f}=(\mu-1)(\frac{1}{R_1}-\frac{1}{R_2})$
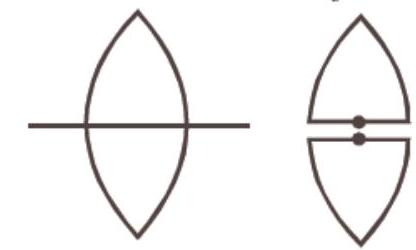
In this case, $R_1$ and $R_2$ are unchanged
So, $f$ will remain unchanged for both pieces of the lens
$\therefore f=f^{\prime}$
$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}$
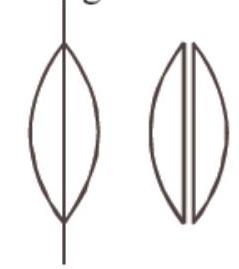
This is combination of two lenses of equal focal lengths
$\therefore \frac{1}{f}=\frac{1}{f^{\prime \prime}}+\frac{1}{f^{\prime \prime}}=\frac{2}{f^{\prime \prime}} \Rightarrow f^{\prime \prime}=2 f$.
A symmetric lens is cut along optical axis in two equal parts. Intensity of image formed by each part will be same as that of complete lens. Focal length is double the original for each part.
