Moving Charges and Magnetism - Result Question 44
45. Two long parallel wires $P$ and $Q$ are both perpendicular to the plane of the paper with distance of $5 m$ between them. If $P$ and $Q$ carry currents of $2.5 amp$ and $5 amp$ respectively in the same direction, then the magnetic field at a point half-way between the wires is
(a) $\frac{3 \mu_0}{2 \pi}$
(b) $\frac{\mu_0}{\pi}$
(c) $\frac{\sqrt{3} \mu_0}{2 \pi}$
(d) $\frac{\mu_0}{2 \pi}$
[2000]
Show Answer
Answer:
Correct Answer: 45. (d)
Solution:
- (d) When the current flows in both wires in the same direction then magnetic field at half way due to the wire $P$,
$ \vec{B} _p=\frac{\mu_0 I_1}{2 \pi \frac{5}{2}}=\frac{\mu_0 I_1}{\pi \cdot 5}=\frac{\mu_0}{2 \pi} \quad(.$ where $.I_1=2.5 amp)$
The direction of $ \vec{B} _p$ is downward $\odot$
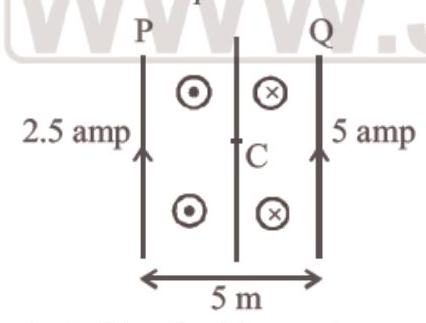
Magnetic field at half way due to wire $Q$
$ \vec{B} _Q=\frac{\mu_0 I_2}{2 \pi \frac{5}{2}}=\frac{\mu_0}{\pi} \quad[$ upward $\otimes]$
[where $I_2=2.5 amp$.]
Net magnetic field at half way
$ \begin{aligned} \vec{B} & =\vec{B} P+\vec{B} Q \\ & =-\frac{\mu_0}{2 \pi}+\frac{\mu_0}{\pi}=\frac{\mu_0}{2 \pi} \quad \text{ (upward) } \end{aligned} $
Hence, net magnetic field at midpoint $=\frac{\mu_0}{2 \pi}$






