Motion in a Straight Line - Result Question 40
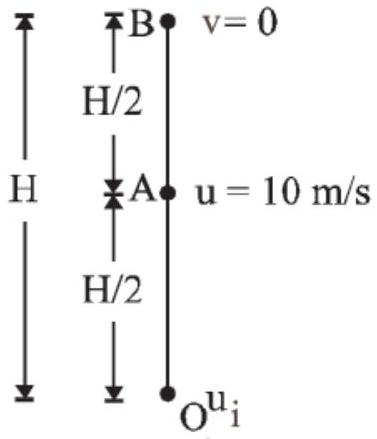
41. Two bodies, A (of mass $1 kg$ ) and B (of mass $3 kg$ ), are dropped from heights of $16 m$ and $25 m$, respectively. The ratio of the time taken by them to reach the ground is
(a) $12 / 5$
(b) $5 / 12$
(c) $4 / 5$
(d) $5 / 4$
[2006]
Show Answer
Answer:
Correct Answer: 41. (c)
Solution:
- (c) Let $t_1 & t_2$ be the time taken by $A$ and $B$ respectively to reach the ground then from the formula,
$h=\frac{1}{2} g t^{2}$,
For first body, $\quad 16=\frac{1}{2} g t_1{ }^{2}$
For second body, $25=\frac{1}{2} g t_2{ }^{2}$
$\therefore \frac{16}{25}=\frac{t_1^{2}}{t_2^{2}} \Rightarrow \frac{t_1}{t_2}=\frac{4}{5}$.
If a body is a dropped from some height, the motion is independent of mass of the body. The time taken to reach the ground $t=\sqrt{2 h / g}$ and final velocity $V=\sqrt{2 g h}$ and initial velocity, $u=0$. (a) For part $A B$
From 3rd equation of motion $v^{2}=u^{2}-2 gH$
$0=u^{2}-2 g(H / 2)=u^{2}-gH$
$H=\frac{u^{2}}{g}=\frac{10^{2}}{10}=10 m$
