Motion in a Plane - Result Question 33
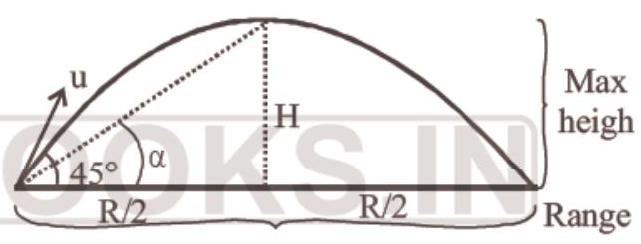
36. A projectile is fired at an angle of $45^{\circ}$ with the horizontal. Elevation angle of the projectile at its highest point as seen from the point of projection is
[2011M]
(a) $60^{\circ}$
(c) $\tan ^{-1}(\frac{\sqrt{3}}{2})$
(b) $\tan ^{-1}(\frac{1}{2})$
(d) $45^{\circ}$
Show Answer
Answer:
Correct Answer: 36. (b)
Solution:
- (b) Maximum height,
$H=\frac{u^{2} \sin ^{2} 45^{\circ}}{2 g}=\frac{u^{2}}{4 g}$
Range, $R=\frac{u^{2} \sin 90^{\circ}}{g}=\frac{u^{2}}{g}$
$\therefore \frac{R}{2}=\frac{u^{2}}{2 g}$
According to the required condition,
$\therefore \tan \alpha=\frac{H}{R / 2}$
Put the volues from equation (1) and (2)
$\Rightarrow \frac{(\frac{u^{2}}{4 g})}{(\frac{u^{2}}{2 g})} \tan \alpha \quad \therefore \alpha=\tan ^{-1}(\frac{1}{2})$
